并查集

什么是并查集

其实并查集这个名称已经完全解释了这个数据结构了

并合并数据查查找数据集数据的集合

即并查集就是一个可以合并数据，也可以查询数据的集合。当然这是个人理解的白话，下面用正儿八经的文字解释（其实就是 Google 搜了下定义）

并查集：是一种树形数据结构，主要用于不交集的合并以及查询问题。有一个联合-查询算法定义了两个用于此数据结构的操作。

众所周知，数据类型包含 数据+操作，数据等下面再详细介绍，这里主要列举下并查集的基本操作

Union：将两个子集合并。例如联合 (1) 和 (5) 集合，合并为一个集合
Find：查找元素的源头，即查找目标节点的根节点。例如查找 (3)

并查集作用

并查集主要用于判断是否连通，简单来说就是判断其中一个节点能否经过任意路径达到另一个节点，如果可达则为连通，反之则为不可连通。例如可以用来判断大家族的亲戚关系关系，连通则为有亲戚关系，反之则无亲戚关系

并查集引入

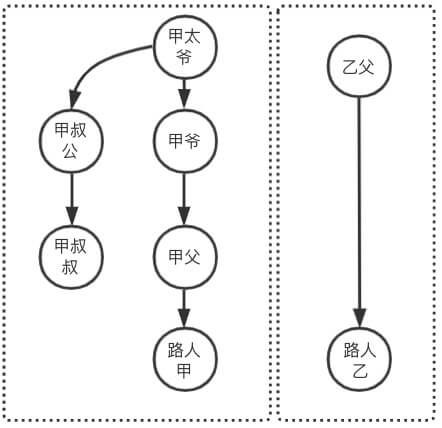
如图所示，如何判断路人甲和路人乙是不是亲戚？

step1 题目分析，路人甲和路人乙是亲戚的条件是 ”祖先是否相同“，那么可将问题转移，表现为 是否为亲戚？ => 祖先是否相同？

step2 继续分析，祖先是否相同其实不好一眼识别，那么可以曲线救国，找出 ”路人甲的祖先和路人乙的祖先，然后对比两个人是否为同一个人”，那么可将问题转移，表现为 祖先是否相同？ => 找出两个人的祖先，然后比较是否相同？

Find 引入

拿路人甲来举例，如何查询路人甲的祖先？根据人的一般思维做出Find 步骤推导

step1 查询路人甲的父亲：路人甲 -> 甲父 step2 查询路人甲的父亲的父亲：甲父 -> 甲爷 step3 查询路人甲的父亲的父亲的父亲：甲爷 -> 甲太爷 step4 查询路人甲…：发现甲太爷上面没人了，那么必然他就是祖先了，则路人甲的祖先就是甲太爷

同理查询出路人乙的祖先是乙父，由于甲太爷 != 乙父，则路人甲和路人乙不是亲戚

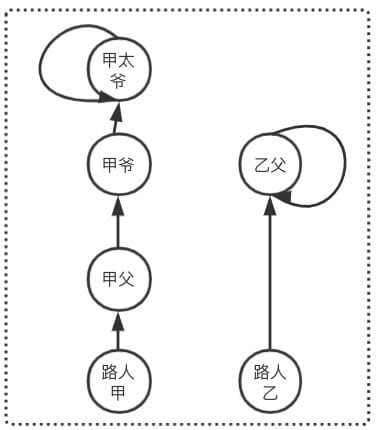
Union 引入

突然有一天，甲爷发现乙父是失散多年的儿子，准备让乙父认祖归宗，则此时甲爷和乙父建立了关系。那么此时路人甲和路人乙是否是亲戚？

按照上述 Find 步骤求得 甲太爷 == 甲太爷，则路人甲和路人乙是亲戚

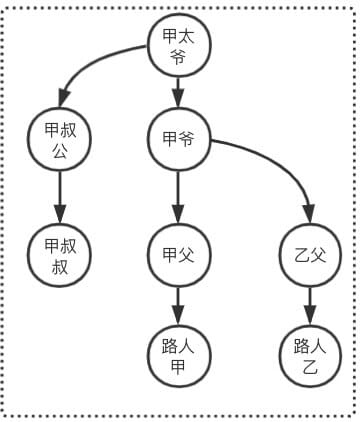
并查集代码实现

数据初始化

对象存储（树形存储）

按照上面绘制的图形，甲太爷下面有甲叔公、甲爷；甲爷下面有甲父；甲父下面有路人甲…，明显得这是一个树形结构

Step1 分析出了树形结构，想都不用想，直接先整个树形结构先

class TreeNode {
  value: number;
  children: TreeNode[] | null; // 不知道子节点有多少个，所以用数组存储
}

Step2 树形结构整出来了，发现有点不对，按照 Find 步骤推导，子级必须可以找到父级，但是这里子级都没有存储父级，不可能从子级找到父级。所以一拍脑壳，没有就加个嘛

class TreeNode {
  value: number;
  parent: TreeNode;
  children: TreeNode[] | null;
}

Step3

打完收工，收工到一半发现还是有点不太对，按照Find 步骤推导，我根本不需要从父级找到子级，只需要从子及级找到父级，那么 children 属性完全是浪费嘛，果断去了

class TreeNode {
  value: number;
  parent: TreeNode;
}

这下就科学多了，存储节点搞定了

数组存储

由 “对象存储” 我们知道了一个关键点：只需要子级找到父级即可，父级不必知道子级，那么可以采用一种更加简单的存储结构数组存储，以数组的 index 表示子节点，以 array[index] 表示该子节点的父节点，表现为 array[index] = parent；根节点的等于自身，表现为 array[root] = root;

class UnionFind {
  private findUnionList: number[];

  constructor(max: number) {
    // 初始化时，让节点全部指向自己，即认为他们全都是独立的
    this.findUnionList = new Array(max + 1).fill(0).map((i, ind) => ind);
  }
}

后续实例代码都使用数组存储来演示噶

Find

根据Find 步骤推导得出以下代码

class UnionFind {
  private findUnionList: number[];

  constructor(max: number) {
    this.findUnionList = new Array(max + 1).fill(0).map((i, ind) => ind);
  }

  find(x: number): number {
    while (x !== this.findUnionList[x]) {
      x = this.findUnionList[x];
    }
    return x;
  }
}

Union

class UnionFind {
  private findUnionList: number[];

  constructor(max: number) {
    this.findUnionList = new Array(max + 1).fill(0).map((i, ind) => ind);
  }

  find(x: number): number {
    while (x !== this.findUnionList[x]) {
      x = this.findUnionList[x];
    }
    return x;
  }

  union(x: number, y: number) {
    const rootX: number = this.find(x);
    const rootY: number = this.find(y);

    this.findUnionList[rootX] = rootY;
  }
}

并查集优化

路径压缩

观察 find 方法，每次 Find 操作时，都需要从子->父->父.父->父.父.父…->根去查找，如果只是几个节点那还好，如果节点数到达 1 千个、1 万个、10 万个…，显而易见的查询效率会越来越低。那么有没得啥子办法来提高查询效率？

我们观察查询步骤，发现父节点对于子节点的意义只是做为跳板，去查询根节点的，并没有其他特殊的意义，那么直接将子节点的 parent 指向根节点，每次检查都只需要一次查询就完工咯。你可以想象成把一颗”高瘦的树变成一棵矮胖的树

既然知道了优化的办法了，下面列举两种不同的实现方法

一步到位

一次 Find 操作，就将该查询链上的节点全部指向根节点

class UnionFind {
  private findUnionList: number[];

  constructor(max: number) {
    this.findUnionList = new Array(max + 1).fill(0).map((i, ind) => ind);
  }

  find(x: number): number {
    if (x === this.findUnionList[x]) return x;
    return (this.findUnionList[x] = this.find(this.findUnionList[x]));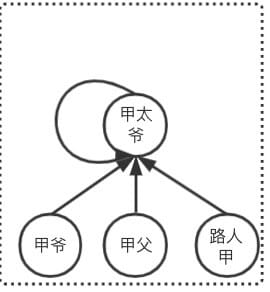
  }
}

循序渐进

如果是一步到位是个激进派，那么循序渐进就是一个保守派。它并不是全部直接指向根节点，而是每次把父级往前移动一个，例如原来是子->父，现在是子->(父->父)，表现为 array[index] = array[array[index]]，子的父级缓慢向前移动，最终指向 root

class UnionFind {
  private findUnionList: number[];

  constructor(max: number) {
    this.findUnionList = new Array(max + 1).fill(0).map((i, ind) => ind); // 初始化时，让节点全部指向自己，即认为他们全都是独立的（全部都是单身狗
  }

  find(x: number): number {
    while (this.findUnionList[x] !== x) {
      const prev = x;
      x = this.findUnionList[x];
      this.findUnionList[prev] = this.findUnionList[x];
    }
    return x;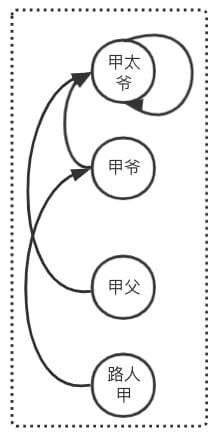
  }
}

按秩合并

我们拿路人甲家族和路人乙家族来说：

原来路人甲 Find 操作需要 4 次查询操作才能完成查询
原来路人乙 Find 操作需要 2 次查询操作才能完成查询

最大查询次数 maxFind = 4

我们现在按照如下两种合并方式

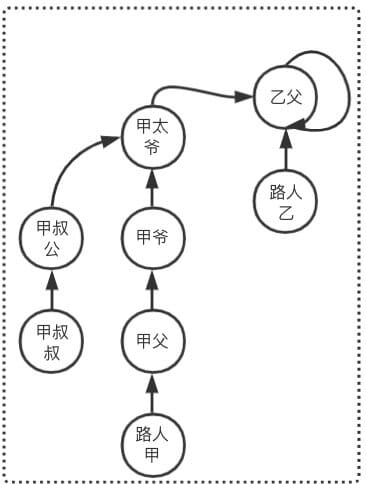
路人甲家族合并到路人乙家族

现在路人甲 Find 操作需要 5 次查询操作才能完成查询
现在路人乙 Find 操作需要 2 次查询操作才能完成查询

最大查询次数 maxFind = 5 比合并前多出了 1 次

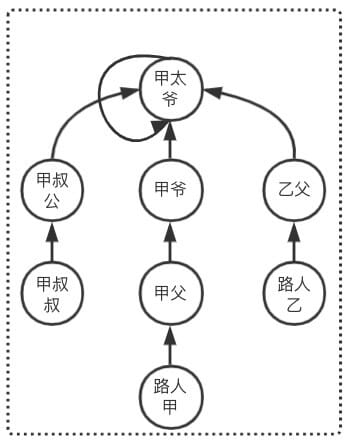
路人乙家族合并到路人甲家族

现在路人甲 Find 操作需要 4 次查询操作才能完成查询
现在路人乙 Find 操作需要 3 次查询操作才能完成查询

最大查询次数 maxFind = 4 保持为合并前最大查询次数

接下来，我们想一想为什么勒，继续回到查询步骤，我们的查询是这样的子->父->(父.父)…->根，这查询次数不就是树的深度嘛

于是我们得到了结论：将深度小的集合合并到深度大的集合可以获得更好的性能

那如果树的深度相同呢？

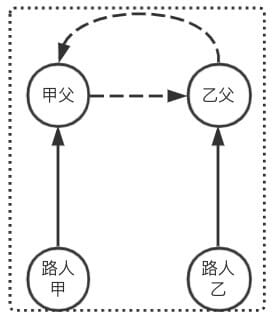
无论是甲父合并到乙父还是乙父合并到甲父，最大查询次数都会增加，由 2 增加为 3，则当树深度相同时，就不用纠结了，谁合并谁都一样，只是深度加 1

那么对上面的结论修正：将深度小的集合合并到深度大的集合可以获得更好的性能，如果集合深度相同，则任意合并，深度+1

对于树形存储的按秩合并

由于需要存储当前树的深度，则需要更新下 TreeNode

class TreeNode {
  value: number;
  parent: TreeNode;
  deep: number;
}

对于数组存储的按秩合并

由于数组已经木有地方存储树的深度了，则需要重新找个存储的地方

class UnionFind {
  private findUnionList: number[]; // 存储节点
  private findUnionDeepList: number[]; // 存储节点深度

  constructor(max: number) {
    this.findUnionList = new Array(max + 1).fill(0).map((i, ind) => ind);
    this.findUnionDeepList = new Array(max + 1).fill(0);
  }

  find(x: number): number {
    while (this.findUnionList[x] !== x) {
      const prev = x;
      x = this.findUnionList[x];
      this.findUnionList[prev] = this.findUnionList[x];
    }
    return x;
  }

  union(x: number, y: number) {
    const rootX: number = this.find(x);
    const rootY: number = this.find(y);

    const deepX: number = this.findUnionDeepList[rootX];
    const deepY: number = this.findUnionDeepList[rootY];

    if (deepX > deepY) {
      this.findUnionList[rootY] = rootX;
    } else if (deepX < deepY) {
      this.findUnionList[rootX] = rootY;
    } else {
      this.findUnionList[rootX] = rootY;
      this.findUnionDeepList[rootY]++;
    }
  }
}