Skip to content
知识库

图形学

图形学就是将真实世界的物体渲染至计算机中。

图形学和计算机视觉的区别

图形学: 将准备好的模型渲染为图片 计算机视觉: 利用计算机去猜测图片，从而将图片转换为模型。

Linear Algebra(线性代数)

Coordinate(坐标系)

坐标系分为很多种，例如笛卡尔坐标系，裁剪坐标系，世界坐标系等等。目前主要了解笛卡尔坐标系和裁剪坐标系，且如果在未说明的情况下，默认遵守右手螺旋定则，拿计算机屏幕来说

  • 原点在屏幕中心，视为 (000)\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}
  • X 轴为水平轴，从原点向右为正，向左为负
  • Y 轴为竖直轴，从原点向上为正，向下为负
  • Z 轴为垂直屏幕，从原点向屏幕外为正，向屏幕内为负

裁剪坐标系和其他坐标系有所区别，它的最大值为 1.0，最小值为-1.0，即其他坐标系需要按照比例缩放至该值

Vector(向量)

向量的作用：描述值和方向

单位向量: 值为 1 的向量，只用来描述方向

Dot Product(点乘)

两个向量点乘，可以生成一个新的标量（数），且向量的点乘，满足于交换律，分配律，结合律

x⃗⋅y⃗=∣∣x∣∣∗∣∣y∣∣∗cos⁡θ\vec{x} · \vec{y} = ||x|| * ||y|| * \cosθ

  • θθ 为两个向量的夹角

也可以通过坐标系来计算

(x1y1z1)⋅(x2y2z2)=x1∗x2+y1∗y2+z1∗z2\begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} · \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = x_1*x_2 + y_1*y_2 + z_1*z_2

  1. 可以用计算两个向量的夹角 θθ（反余弦函数）
    1. 判断两个向量是否同向：值为正，则为同向；否则为反向
    2. 判断两个向量是否靠近：值越大，则越接近
  2. 可以求向量的分解，例如计算 的投影

Cross Product(× 乘)

x 乘，生成了另一个向量

新向量的方向：为垂直于 a,b 向量的平面，以右手螺旋定则，四指指向 a 向量旋转至 b 向量的方向，拇指即为新向量方向

新向量的模长：为 ∣a×b∣=∣a∣∗∣b∣∗sinθ∣a×b∣=∣a∣*∣b∣* sinθ

向量的 x 乘，并不满足于交换律，按照右手螺旋定则，如果产生交换的话，新的向量方向是相反的，但任然存在分配律和结合律

  1. 可以用来定义三位坐标体系
  2. 可以用来判断 x⃗\vec{x} 在 y⃗\vec{y} 的左侧还是右侧。例如可以检测多边形是凹还是凸
  3. 判断包含关系。例如可以用来判断 1 个点 a，在由 3 个点组成的三角形内还是外

Matrix(矩阵)

矩阵以(M,N)(M,N) 来表示，M 行 N 列。

矩阵加减法必须满足都是(M,N)(M,N)，M3[i][j]=M1[i][j]±M2[i][j]M3[i][j] = M1[i][j] \plusmn M2[i][j]

矩阵比较重要的应用是乘法，但乘法必须满足该条件 (M,N)(N,P)=(M,P)(M,N)(N,P) = (M,P)。即一个 M 行 N 列的矩阵乘以 N 行 P 列的矩阵，最终为 M 行 P 列。

矩阵 M1 乘以 M2 = M3，M3[i][j] 的值为 M1[i]（M1 的第 i 行） 点乘 M2[j]（M2 的第 j 列）

[x1y1z1][x2y2z2]=[x1∗x2x1∗y2x1∗z2y1∗x2y1∗y2y1∗z2z1∗x2z1∗y2z1∗z2]\begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix} \begin{bmatrix} x_2 & y_2 & z_2 \end{bmatrix} = \begin{bmatrix} x_1*x_2 & x_1*y_2 & x_1*z_2 \\ y_1*x_2 & y_1*y_2 & y_1*z_2 \\ z_1*x_2 & z_1*y_2 & z_1*z_2 \end{bmatrix}

逆矩阵

矩阵乘法的逆运算得到的新矩阵，用 M−1M^{-1} 来表示。逆矩阵具有如下特点

  1. 只有 n * n 的矩阵才有逆矩阵
  2. 只有非奇异矩阵才有逆矩阵，即矩阵中的值不能为 0
  3. 矩阵相乘为单位矩阵 M−1∗M=I M^{-1} * M = I

用途

  1. 解线性方程组：对于 y=A∗xy = A * x，如果 A 可逆，则 x=A−1∗yx = A^{-1} * y
  2. 几何变换：撤销某个变换

转置矩阵

将行列互换，则为矩阵的转置，用 MtM^{t} 或者 M′M^{'} 表示。转置矩阵具有如下特点

  1. 任何 n * m 矩阵都有转置矩阵
  2. (Mt)t({M^t})^t = M

用途

  1. 表示向量的点积，dot(u,v)=ut∗vdot(u, v) = u^t * v，两个向量的点积，等于将第一个向量转置后的乘法后的标量相等

Transform 变换

Linear Transformation(线性变换二维)

可以通过矩阵乘法直接完成的变换操作

Scale(缩放): SxS_x, SyS_y 为缩放因子

[Sx00Sy][x1y1]=[x2y2]\begin{bmatrix} S_x & 0 \\ 0 & S_y \\ \end{bmatrix} \begin{bmatrix} x_1 \\ y_1 \\ \end{bmatrix}= \begin{bmatrix} x_2 \\ y_2 \\ \end{bmatrix}

Rotate(旋转): 绕着原点，方向为顺时针旋转，θθ为旋转角度

[cos⁡θ−sin⁡θsin⁡θcos⁡θ][x1y1]=[x2y2]\begin{bmatrix} \cosθ & -\sinθ \\ \sinθ & \cosθ \end{bmatrix} \begin{bmatrix} x_1 \\ y_1 \end{bmatrix}= \begin{bmatrix} x_2 \\ y_2 \end{bmatrix}

Shear(切变): 沿着 X 正方向，例如将一个矩形拉成平行四边形，切变移动 α\alpha

[1α01][x1y1]=[x2y2]\begin{bmatrix} 1 & \alpha \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ y_1 \end{bmatrix}= \begin{bmatrix} x_2 \\ y_2 \end{bmatrix}

Nonlinear Transformation(非线性变换)

Transform(平移): 平移是无法通过一个矩阵乘法计算而得，而是需要通过加法

[x1y1]  − [txty]=[x2y2]\begin{bmatrix} x_1 \\ y_1 \end{bmatrix} \ \ - \ \begin{bmatrix} t_x \\ t_y \end{bmatrix}= \begin{bmatrix} x_2 \\ y_2 \end{bmatrix}

所以想要将所有变化统一为一种表示方法，即用坐标乘以矩阵的形式，目前是做不到的，引入了齐次坐标

Homogeneous Coordinate(齐次坐标)

引入了一个额外的参数，即二维需要三个参数，三维需要四个参数 (xyw)\begin{pmatrix} x \\ y \\ w \end{pmatrix}

(xyzw)\begin{pmatrix} x \\ y \\ z \\ w \end{pmatrix}

齐次坐标表示一个向量（二维）

(xy0)\begin{pmatrix} x \\ y \\ 0 \end{pmatrix}

齐次坐标表示一个点（二维）

(xy1)\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}

且当 w 不为 1 的时候，需要将坐标标准化，即会 x=x wy=y/wx = x \ w \\ y = y / w

借助齐次坐标，可以表示平移，x 平移TxT_x，y 平移TyT_y

[10Tx01Ty001]\begin{bmatrix} 1 & 0 & T_x \\ 0 & 1 & T_y \\ 0 & 0 & 1 \\ \end{bmatrix}

当前其他的变换矩阵同样也可以以齐次坐标表示，例如缩放

[Sx000Sy0000]\begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}

复杂变换

目前的变换都是根据原点计算而得，那么如何计算物体绕着其他的点旋转呢，例如如何计算物体绕着自身中心旋转呢

  1. 将旋转中心平移到原点，物体也需要随之平移
  2. 执行旋转操作
  3. 将旋转中心平移回原位，物体也需要随之平移

借助矩阵的分配律，可以先将次变换的矩阵先行计算出来，最后再去乘坐标，以减少冗余计算

如果同时存在多个运动，常用的计算方式是 缩放 —> 旋转 —> 平移 依次计算（缩放，旋转，平移的计算顺序比较符合人的直观感受）

View Transformation(视图变换)

可以将图形学想象一次毕业合照，人群代表了准备好的模型，摄像机同为摄像机。那么拍一次毕业照需要经过如下步骤

  1. 人群站好自己的位置: 可以类比为准备好一堆模型（模型变换）
  2. 摄影师站好自己的位置: 可以类比为准备好相机（视图变换）
  3. 按下快门进行拍摄: 可以类比为进行一次投影（投影变换）
  4. 打印图片: 可以类比为进行一次光栅化，将 3D 的模型显示在 2D 屏幕上

根据物理的概念相对位置可以知晓，如果相机和模型的相对位置不变，无论他们处于什么位置，拍摄出来的照片肯定都是一致的。所以我们可以固定相机的位置，想拍摄不同的照片的话，就移动模型的位置

我们通过三个向量来描述相机的位置

  1. 相机的位置
  2. 相机的拍摄方向
  3. 相机向上的方向

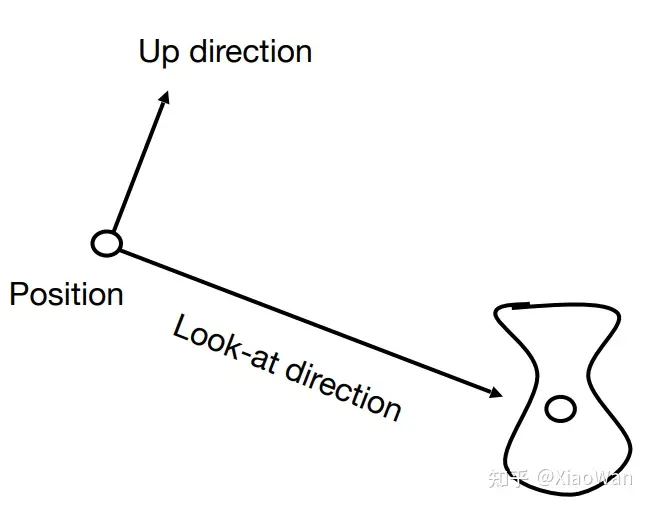
默认相机的位置在**原点，**默认拍摄方向为 -Z，相机向上的方向为+Y

那么如果相机的位置不在原点或者向上的位置不在+Y 该怎么办呢？借助前面的所说的变换，例如不在原点，可平移至原点；向上方向不是+Y，可旋转至该方向

Projection(投影)

投影就是将 3D 物体投射到 2D 平面上的过程，主要分为正交投影和透视投影

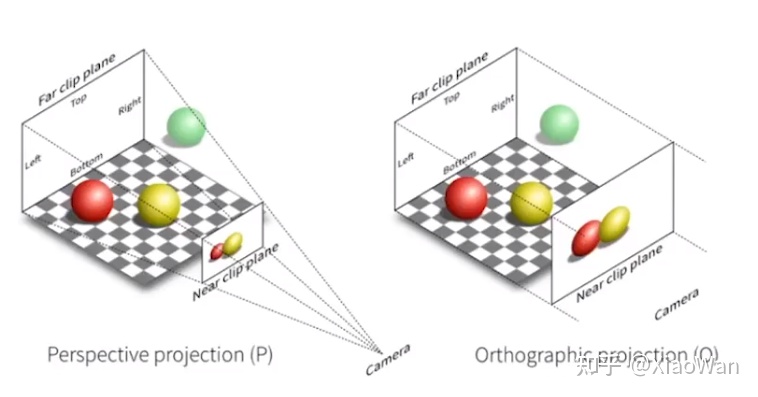
Rectangular Projection(正交投影)

认为光源是从很远的方向打来，是以平行光的方式照射物体，由于是平行光，则不会出现近大远小的情况，而是同样的大小。主要用于绘图等。

如何处理正交投影，分为如下两个步骤

  1. 平移: 由于正交投影是不会改变物体大小的，所以可以直接将投影移动到屏幕上
  2. 缩放: 将投影后的图形缩放为标准图形

标准图形: 在 X,Y,Z 方向都为 1 的立方体

Perspective Projection(透视投影)

认为光源是一个点光源，则在投影的过程中，则会出现近大远小的情况，用于模拟人的眼睛去看物体。可以想象两条铁轨，铁轨是不会相交的，但是眼睛看来，在远处铁轨相交了

如何处理透视投影呢，透视投影的矩阵如下所示，接下来推导求值的过程

[ABCDEFGHIJKLMNOP]\begin{bmatrix} A & B & C & D \\ E & F & G & H \\ I & J & K & L \\ M & N & O & P\\ \end{bmatrix}

透视投影可以根据小孔成像来解释和计算

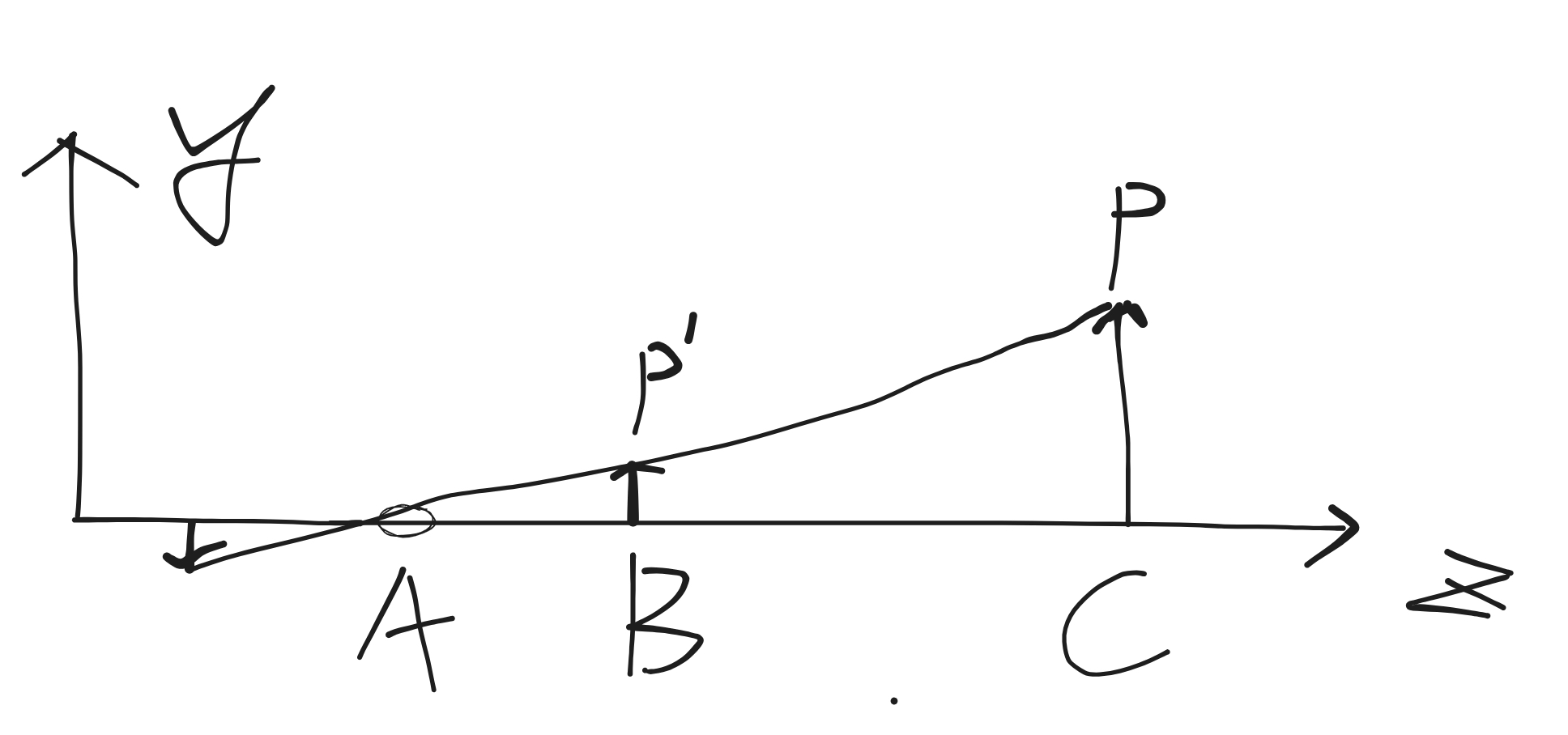
根据小孔成像，一个物体经过小孔成像后，影像是倒立的，不便于计算，在图形学中，可以通过将影像往前移动，移动到和小孔成像距离相同的位置，则可以得到一个方向和原物体一致，且大小和小孔成像一样大小的投影

设原物体坐标(齐次坐标)为

(xyz1)\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}

根据相似三角形的原理，原物体的点 x,y 投影后的位置

y′=y∗ABACy' = \frac{y * AB}{AC}

将 AB 距离记为 n。AC 的距离为已知，且由于相机的位置总是在原点，确朝向的是 -Z 的方向，则 AC 的坐标 Z 的方向是负的，则上述公式可记为。且同理 x’ 坐标也是一样的

y′=y∗n−zy' = \frac{y * n}{-z}

x′=x∗n−zx' = \frac{x * n}{-z}

利用齐次坐标，将除以 -z 的操作，转换为将 w 的值赋予 -z，根据上述公式可以推断出 x,y 行对应的矩阵值

[n0000n00IJKL00−10]\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ I & J & K & L \\ 0 & 0 & -1 & 0 \\ \end{bmatrix}

对于 z 坐标，由于需要映射到[−1,1][-1,1]的区间，则 z 的公式按照矩阵可以得出

z′w=I∗x+J∗y+K∗z+L−z\frac{z'}{w} = \frac{I * x + J * y + K * z + L}{-z}

由于 H 和 I 是 x,y 的坐标，不会对 z 产生影响，则 H,I 为 0

公式为

z′w=K∗z+L−z\frac{z'}{w} = \frac{ K * z + L}{-z}

矩阵值为

[n0000n0000KL00−10]\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & K & L \\ 0 & 0 & -1 & 0 \\ \end{bmatrix}

由于在最 Z 轴的最近端映射到-1，最远段映射到 1

1=K∗f+L−(−f)−1=K∗n+L−(−n)1 = \frac{ K * f + L}{-(-f)}\\ -1 = \frac{ K * n + L}{-(-n)}

  • f: 表示 Z 轴可见的最远 d 位置
  • n: 表示 Z 轴可见的最近的位置

解出该二元一次方程组，可得 K、L

[n0000n0000−f+nf−n−2f∗nf−n00−10]\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2f*n}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix}

此矩阵未对 X、Y 轴进行裁剪，对 X、Y 裁剪的话，可以指定投影面上下左右的边界值，然后对其进行一次缩放平移操作，但是实际操作中，很少会直接定义投影面的上下左右边界，而是定义视角，根据视角大小和 n，以及长宽比，我们可以自行计算投影面的边界。这也是很多库中的 lookAt 的传参

Rasterization(光栅化)

光栅化其实就是将图形转化为像素网格，例如绘制在屏幕上

屏幕

什么是屏幕？一种典型的光栅化设备，有如下特点

老式的 CRT 屏幕是由电子激发荧光屏发光。针对整个屏幕来说，从左上角开始到右下角进行一次线性扫描，就可显示出图像，当每秒经过多次扫描后，即可形成视频。由于荧光屏只有发光和不发光两种状态，则只能显示黑白色

Pixel(像素): 基本显示单元，一般认定一个像素在单位时间只显示一种颜色（虽然事实不是这样，和显示器的排列有关，但可以近似的去理解），每一个像素点可以通过 Red、Green、Blue 来合成显示其他的颜色

将像素和屏幕综合起来看的话

  1. 以(x, y)来描述一个像素
  2. 像素的范围由(0, 0)~(width -1, height-1)，即覆盖的是整个屏幕
  3. 每一个像素的中心电视(x+0.5, y+0.5)

现代显示器从左上角到右下角是由无数个像素组成（每英寸的像素点的个数即为分辨率），由无数个像素点来组成一张图片。现代显示器在内存（显存）开辟一块存储区域 Frame Buffer，用于映射到屏幕，简单来说屏幕怎么显示是受 Frame Buffer 控制的

常用的有如下分类

  1. LCD(液晶显示器)
  2. LED(发光二极管)
  3. OLED
  4. Electronic Ink(电子墨水)：通过电来控制白色墨水（显示白色）在上还是黑色墨水在上（显示黑色）

Sampling(采样)

那么如何能在屏幕上显示一个完整的图形呢？例如在屏幕中间显示一个三角形

最简单的方法就是，遍历屏幕的每一个像素点，如果三角形占据了该像素点，那么这个像素点就发光，反之则不发光，这就是采样

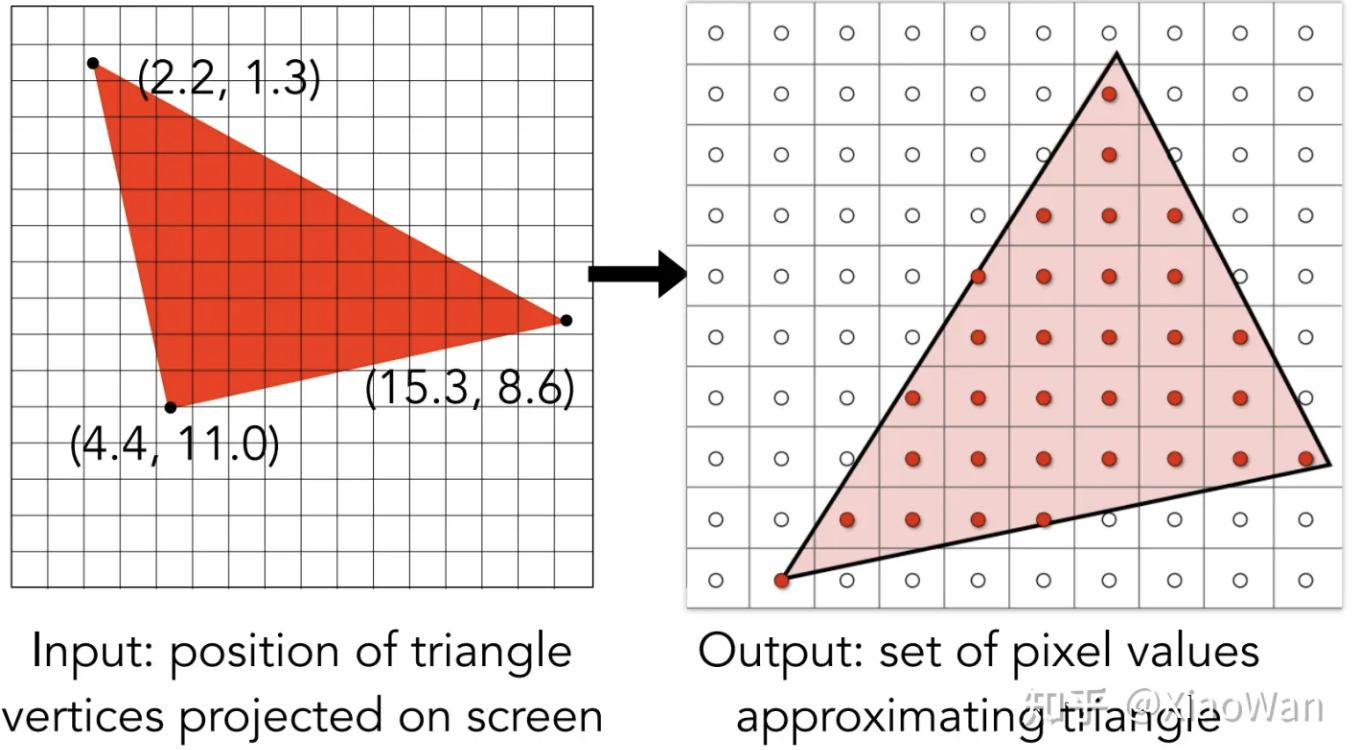
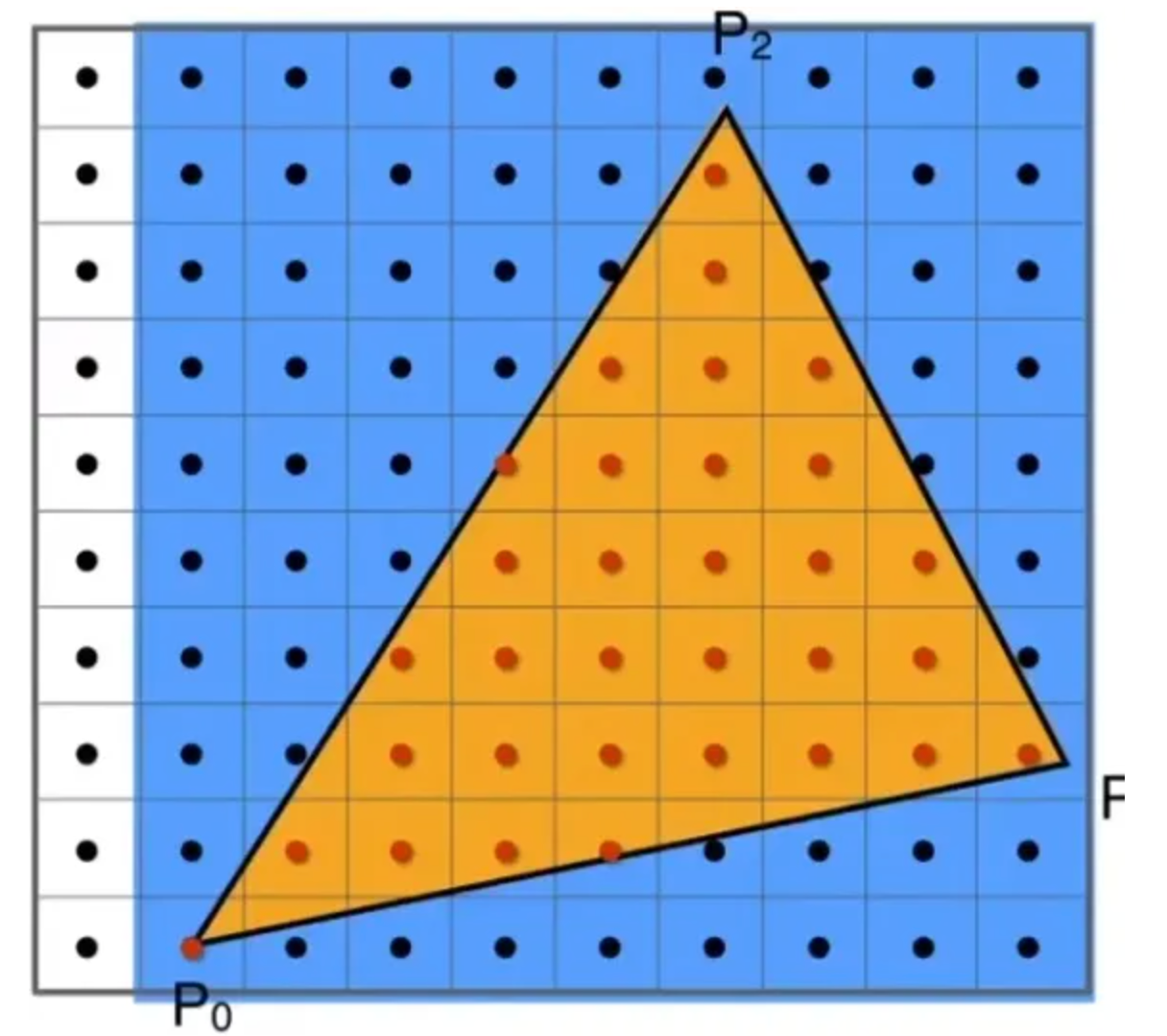
  1. 如何判断三角形是否占据了该像素点: 知道三角形的三个顶点，知道像素点，可以用上面提到过的，向量的 Cross Product，
  2. 有的像素点被三角形只占据了部分怎么办: 我们可以暂定这种没有完全占据的像素点不发光

当然，我们这个三角形并非充满了整个屏幕，所以遍历整个屏幕的像素点比较浪费性能，所以我们只需要遍历此三角形的 Bounding Box(包围盒) 即可，而不用遍历整个屏幕

Aliasing(采样瑕疵、走样)

拿我们上边采样来说，三角形的边不可能完美的按照像素排列，所以肯定有的像素点并没有被三角形完全占据，无论我们定义这部分的像素发光与否，最终都会形成如下

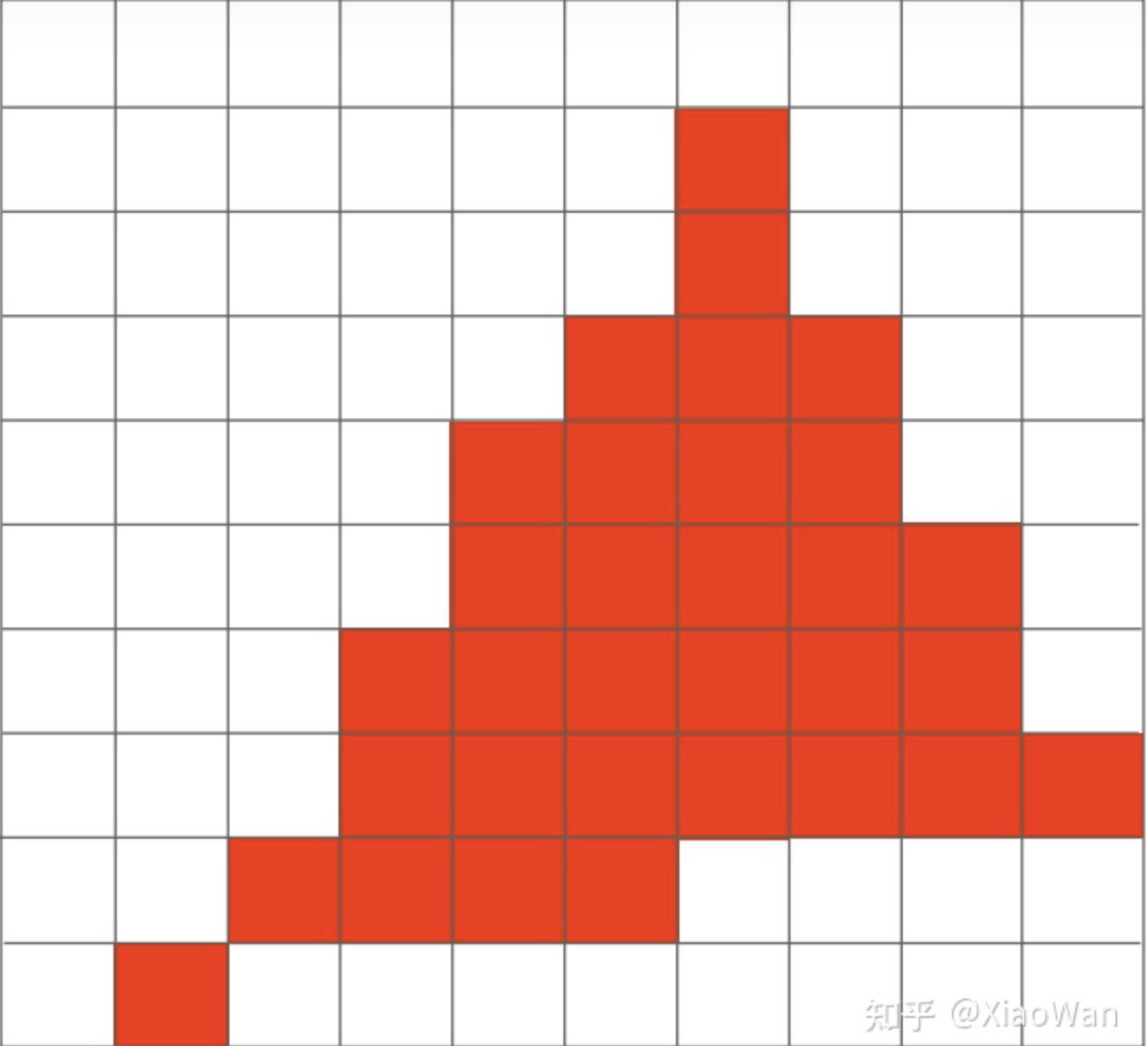
可以看待这里存在明显的锯齿，这就是采样瑕疵。生活中也有许多采样瑕疵，举个例子

  1. 锯齿
  2. 摩尔纹
  3. 车轮效应

Anti-Aliasing(反走样)

常用的反走样有很多方式，以下简单列举下

  1. 增加采样率，即将像素点分的足够小，足够密集，人眼则无法观看到锯齿
  2. 超采样
  3. 抗锯齿，目前常用的

抗锯齿的处理步骤如下

  1. 模糊处理: 先将图片模糊处理
  2. 对每个像素进行采样

那么如何对图片进行模糊处理呢？

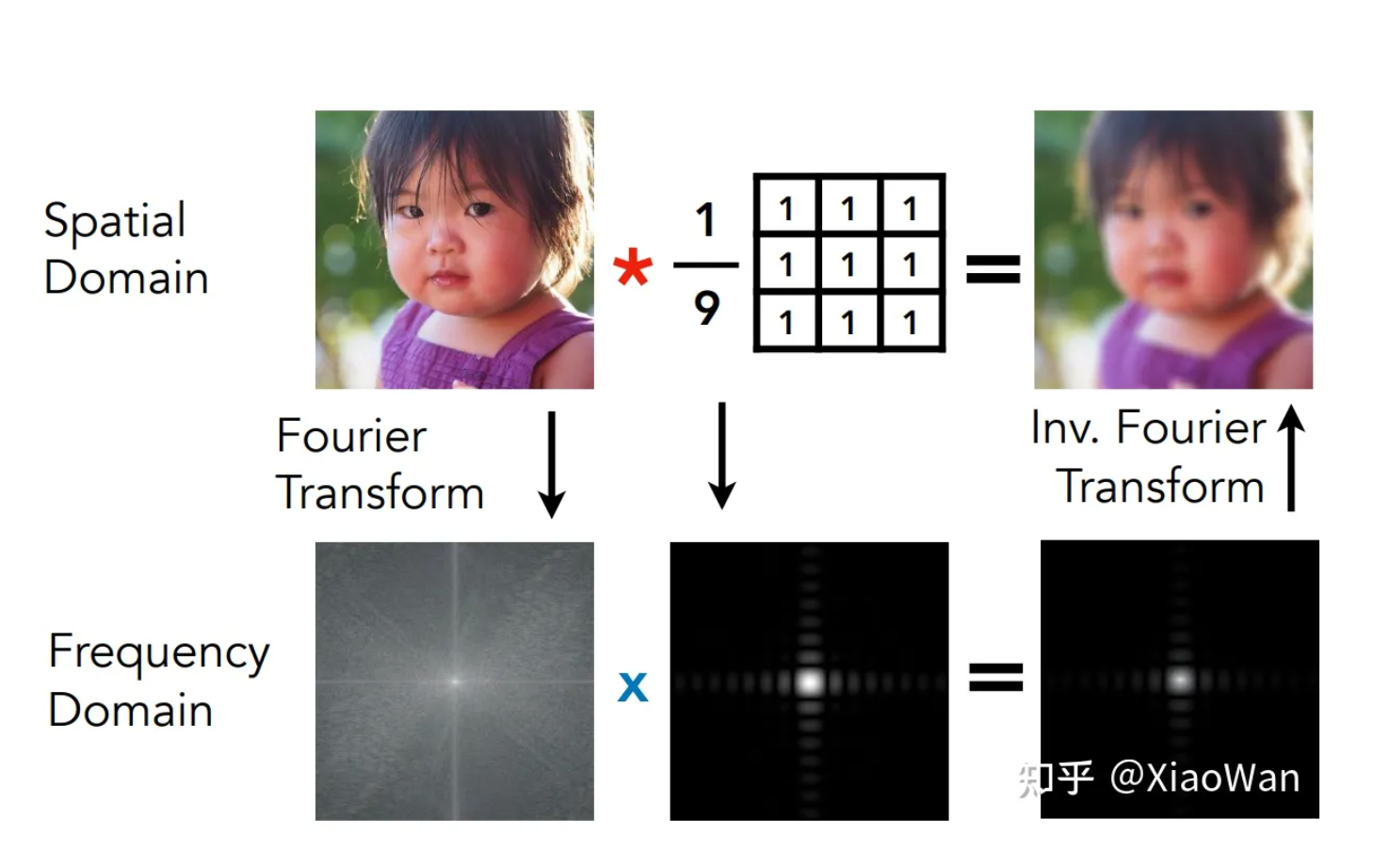
在时域上的一张图片，可以根据傅里叶变换，变换为一张频域的照片，再去掉高频的（相差很大的），再经过逆傅里叶变换，则可以获得一张模糊的图片，整个操作称为滤波。在实际操作中，使用一个卷积核去卷积三角形的每个像素

滤波：删除特点的频率

  1. 高通滤波：只显示高频的信息，即锐化
  2. 低通滤波：只显示低频的信息，即模糊化

这里的 卷积 == 滤波 == 平均

那么如何对每个像素进行采样呢？例如对某个像素点，三角形占用大部分和占用小部分时颜色该如何计算呢？ 假设在一个像素内，该三角形占 25%，则此处颜色为 25% 的三角形颜色，如果占 50%，则此处颜色为 50% 三角形的颜色，依次类推。但是这种得到占比的算法非常复杂，虽然得到精确的占有率非常困难，但是可以使用一个较为简单的方法来得到近似解

MSAA(多重采样抗锯齿)，在一个像素内多增加一些采样点，例如将一个像素变成 4 个采样点，再分别计算每个采样点是否被三角形覆盖，最终合一起就是一个像素的近似数据。和超采样抗锯齿（SSAA）的区别是

  1. 超采样抗锯齿：是真实的生成了多倍像素，GPU 也会增加相对应的执行次数，所以性能消耗较大
  2. 多重采样抗锯齿：还是原来的像素个数，只是在一个像素内，增加了多倍的采样点，再将多个采样点颜色混合，Shader 的执行次数几乎不变

可见性

当两个物体出现遮挡时，原则上必然是近处的物体遮挡远处的物体，那么在绘制时如何判断

画家算法

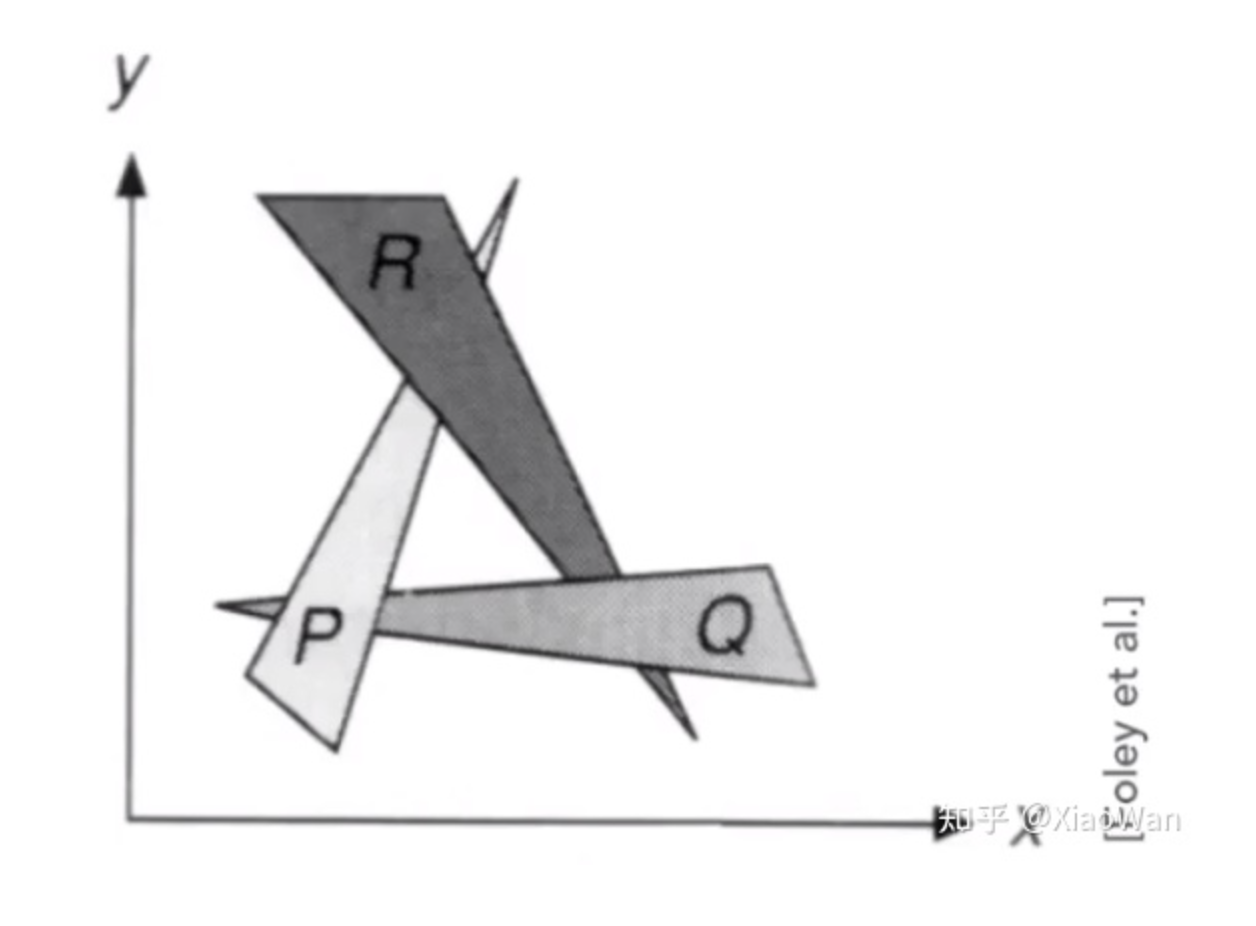
根绘画的经验，先绘制远处的，再绘制近处的，然后近处的物体则会覆盖掉远处的。画家算法优点是比较简单，但是无法处理较为复杂的情况，例如当物体出现交叉，则回家算法无法准确绘制

Z-Buffer(深度测试)

深度图

储存每个像素对应的最浅的深度。使用 Z-Buffer 来保存每一个像素点的最浅的深度信息，当对图形的某个像素点绘制时，比较图形在当前像素点的深度和 Z-Buffer 存储的深度（请注意此处用的是深度，由于物体总是处于-Z 轴，取深度的需要注意正负号）

  • 图形在当前像素点的深度 < Z-Buffer 存储的深度: 渲染当前图形，并更新 Z-Buffer
  • 不做操作

在极端情况下，Z-Buffer 值相同该如何处理呢？如果 Z-Buffer 相同，则很容易出现一些闪烁的问题(Z-Fighting)，可以采取如下方式解决

  1. 使用精度更高的 Z-Buffer。例如原来 Z-Buffer 保存 24 位，可以调整为保存 32 位
  2. 避免将图形放在非常非常近的面上
  3. 可以将图形偏移(Polygon Offse)。渲染前将图形微小偏移

结果图

储存最终的结果

Shading(着色)

对不同物体应用不同的材质(Material)

Blinn-Phone Reflectance Model(Blinn-Phone 反射模型)

  1. Specular highlights(高光)
  2. Diffuse reflection(漫反射)
  3. Ambient lighting(间接/环境光)
Diffuse reflection(漫反射)

漫反射有如下特点

  1. 受光源的距离影响。物体离光源越远，则光线强度越弱，由于光线照射为一个球，设在单位距离的光照强度为I0I_0,则在距离光源距离 r 的位置强度公式为

I1=I0∗(4π/4πr2)=I1=I0/r2I_1=I_0 * (4\pi / 4\pi r^2) \\ = \\ I_1=I_0 / r²

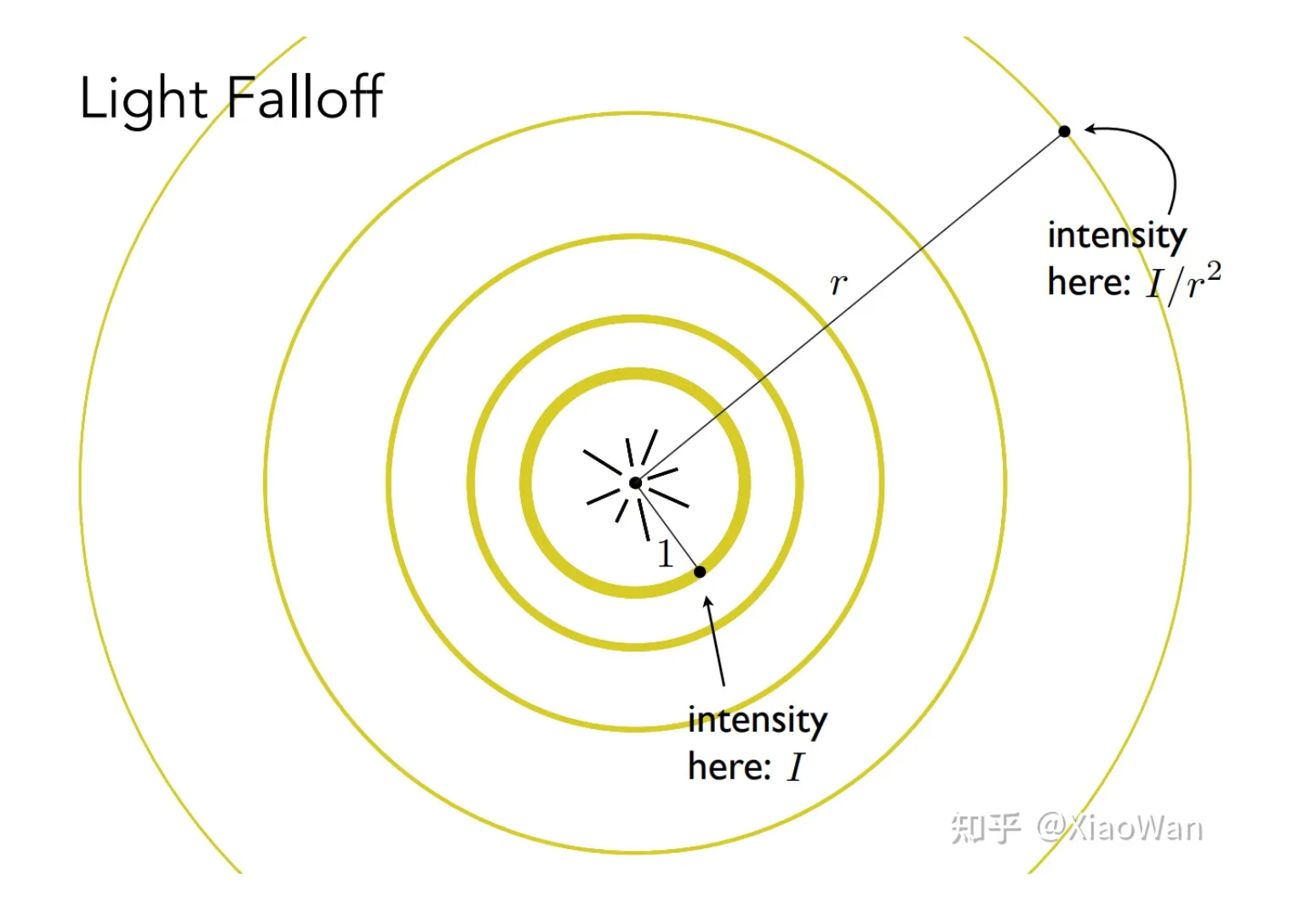
picture 9

  1. 受光线入射方向、物体法线影响。

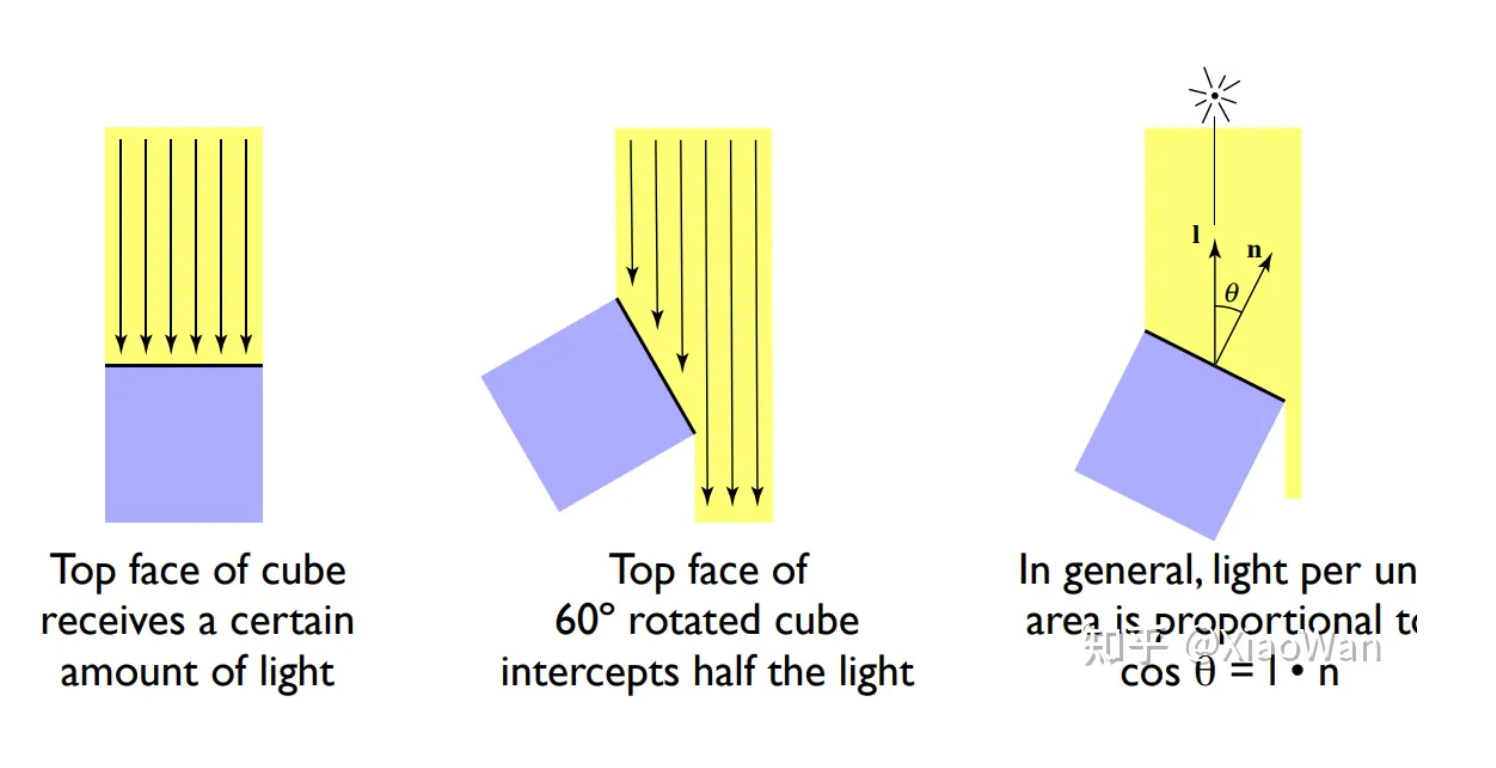
  1. 受物体本身影响。物体把不能吸收的都反射出去了，然后眼睛看起来就是这个颜色
  2. 漫反射想象为一束光照射到物体上，均匀的反射到各个方向，即各个观察角度观察到的光是一样的

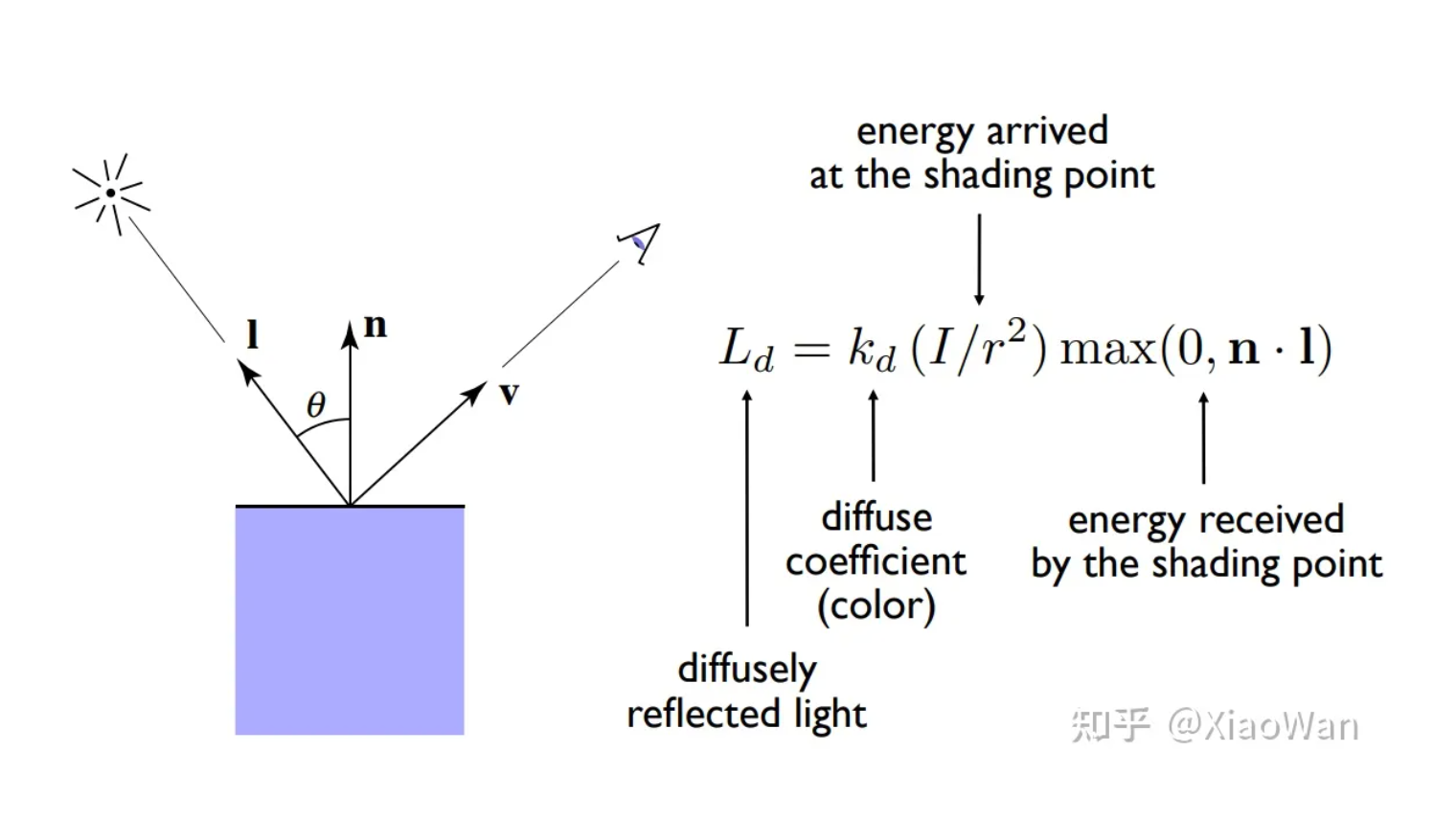
Ld=kd(I/r2)max(0,n⃗⋅l⃗)L_d = k_d(I / r^2)max(0, \vec{n} · \vec{l})

  • LdL_d可以被观察到的漫反射的光
  • kdk_d 漫反射系数，表示的单位区域会反射哪种颜色
  • II 表示光源在单位距离的能量
  • rr 表示单位区域距离光源的距离
  • nn 表示单位区域的法线向量
  • ll 表示单位区域到光源的向量
Specular highlights(高亮、镜面反射)
  1. 受光源距离的影响
  2. 受光线入射方向、物体法线、观察方向影响，由于是镜面反射，则法线方向必须是入射方向和观察方向组成的角的角平分线
  3. 受物体本身影响

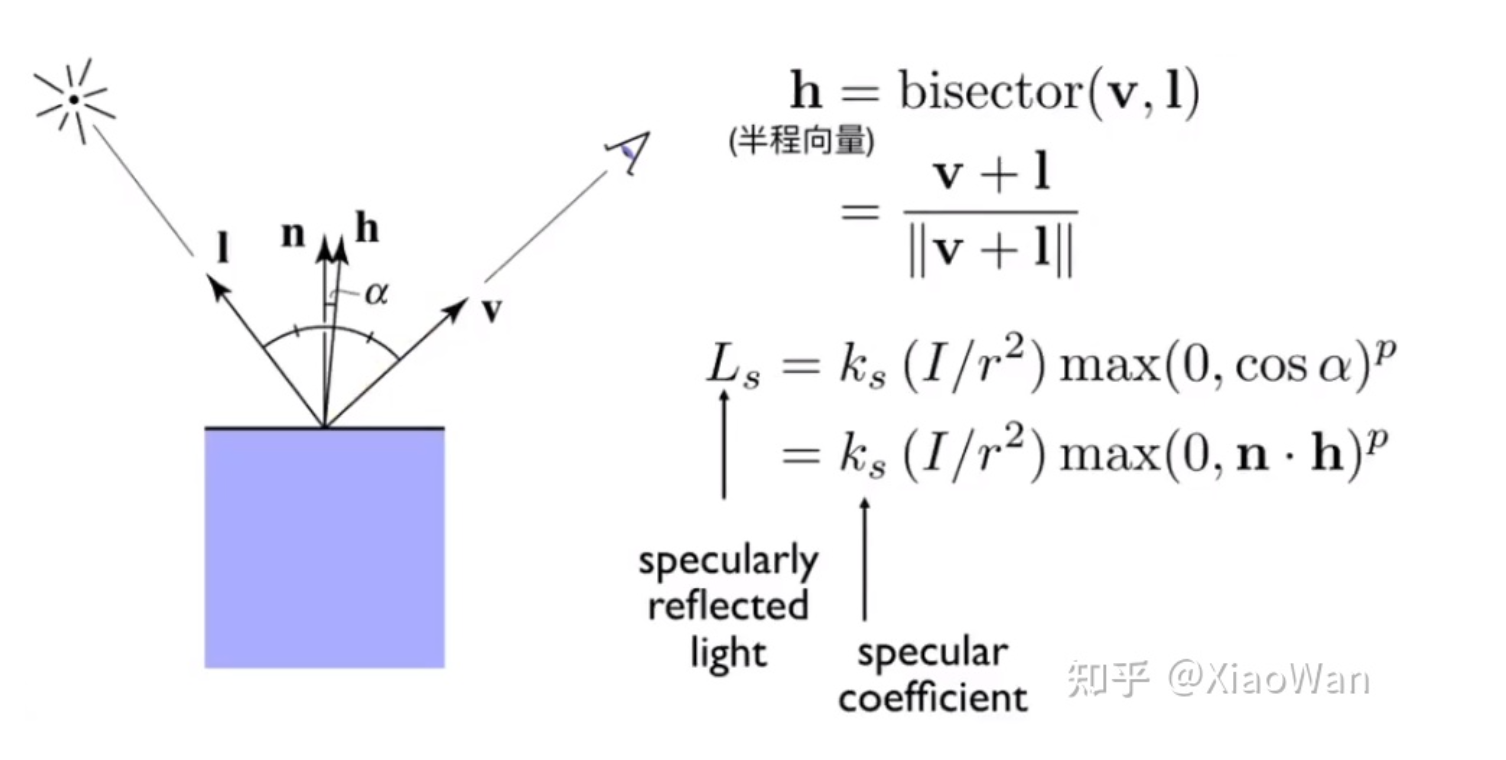
picture 12

Ls=ks(I/r2)max(0,n⃗⋅h⃗)pL_s = k_s(I/r^2)max(0,\vec{n} · \vec{h})^p

  • LsL_s可以被观察到的镜面反射光
  • ksk_s 镜面反射系数
  • II 表示光源在单位距离的能量
  • rr 表示单位区域距离光源的距离
  • nn 表示单位区域的法线向量
  • hh 表示单位区域到光源、单位区域到相机的半程向量
  • pp 由于cos⁡θ\cosθ变换区间太小了，使用幂来增大变化区间
Ambient lighting(环境光)

环境光非常难于计算，所以认为环境光是四面八方照射而来，且与入射方向，法线，观察方向无关

  1. 受光源影响
  2. 受物体本身影响

La=kaIaL_a = k_a I_a

  • LaL_a可以被观察到的环境光
  • kak_a 环境光系数
  • IaI_a 表示光源在物体的能量

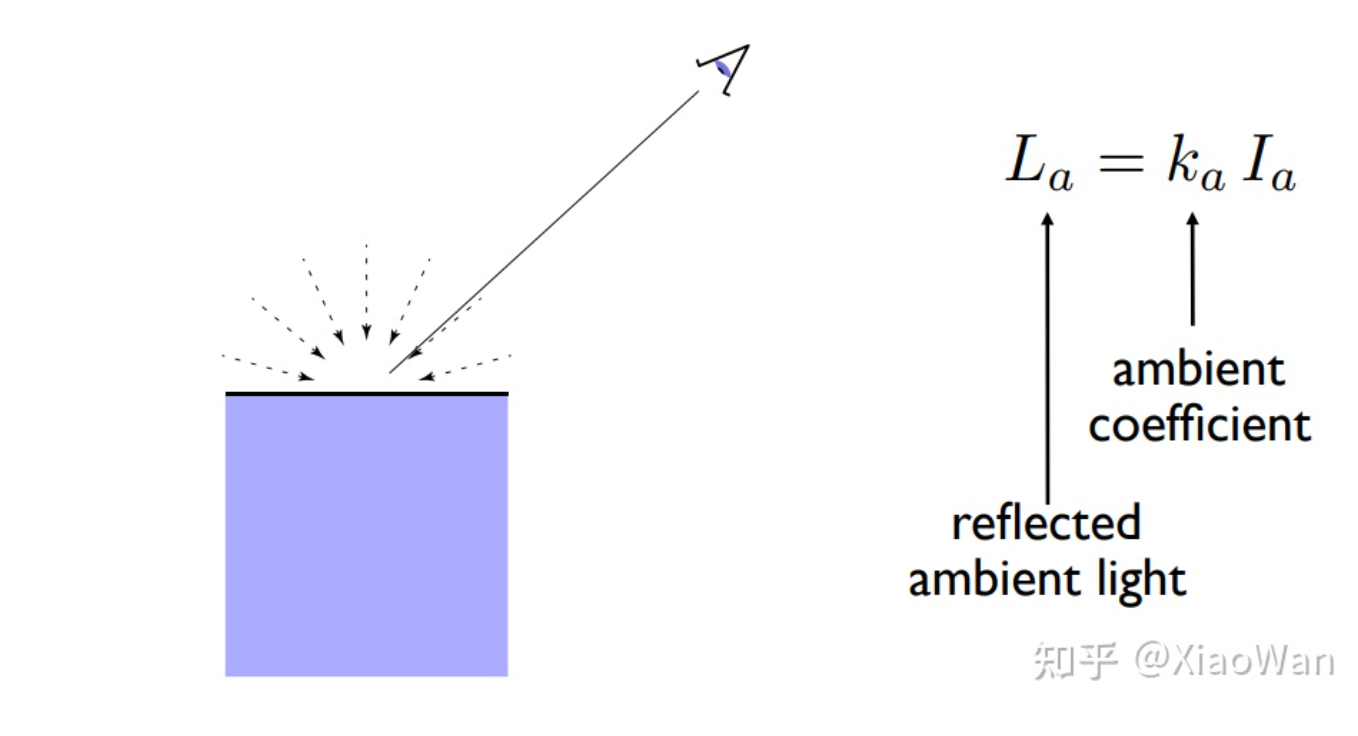
总公式为

L=Ld+Ls+LaL = L_d + L_s + L_a

Shading Frequencies(着色频率)

着色到底应用于那些点

  • Flat Shading 着色于一个平面
  • Gouraud Shading 着色于每一个顶点
  • Phone Shading 着色于每一个像素

一般来说，着色频率越高，效果越高，计算量也更大。但事实无绝对，并非是 Flat Shading 效果就一定差，当物体的面足够多，分得足够细，效果也是非常好的

目前 webGL 着色频率为 Gouraud Shading（顶点着色器） + Phone Shading（片元着色器根据顶点着色器算每个像素的差值）

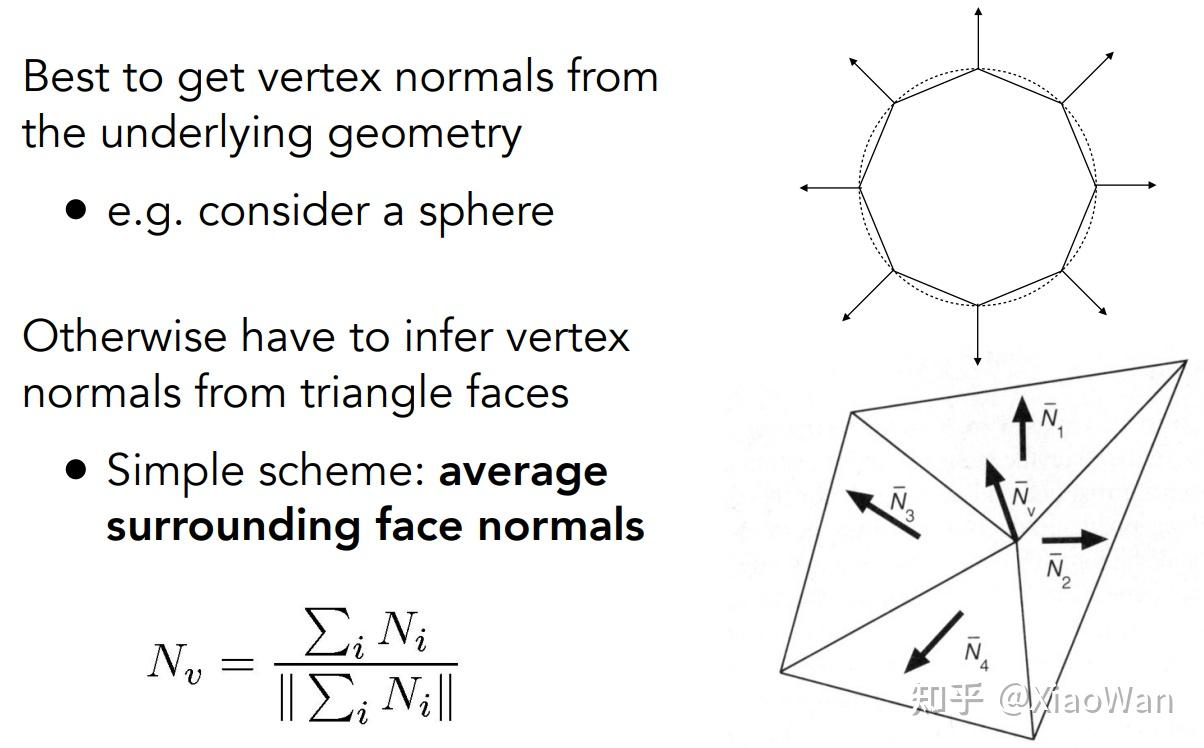
如何去计算一个顶点的法线

如果一个顶点在正方体上，就比较好计算，那如果在复杂图形中呢。在复杂图形中，取顶点周围的面的法线，进行加权平均

那如何计算一个面的法线呢，这就要用到向量的 × 乘了，取一个面上的三个点，两两组成向量，× 乘即可获取平面的法线（右手螺旋定则）

Real-time Rendering Pipeline(实时渲染管线)

目前渲染管线都是在 GPU 中被编程完成了，只有顶点处理和片段处理可以编程。整个步骤如下

  1. 输入空间中一系列的点
  2. 顶点处理
  3. 三角形处理
  4. 光栅化
  5. 着色
    1. 片段（像素）处理
    2. 帧缓冲区处理
  6. 输出

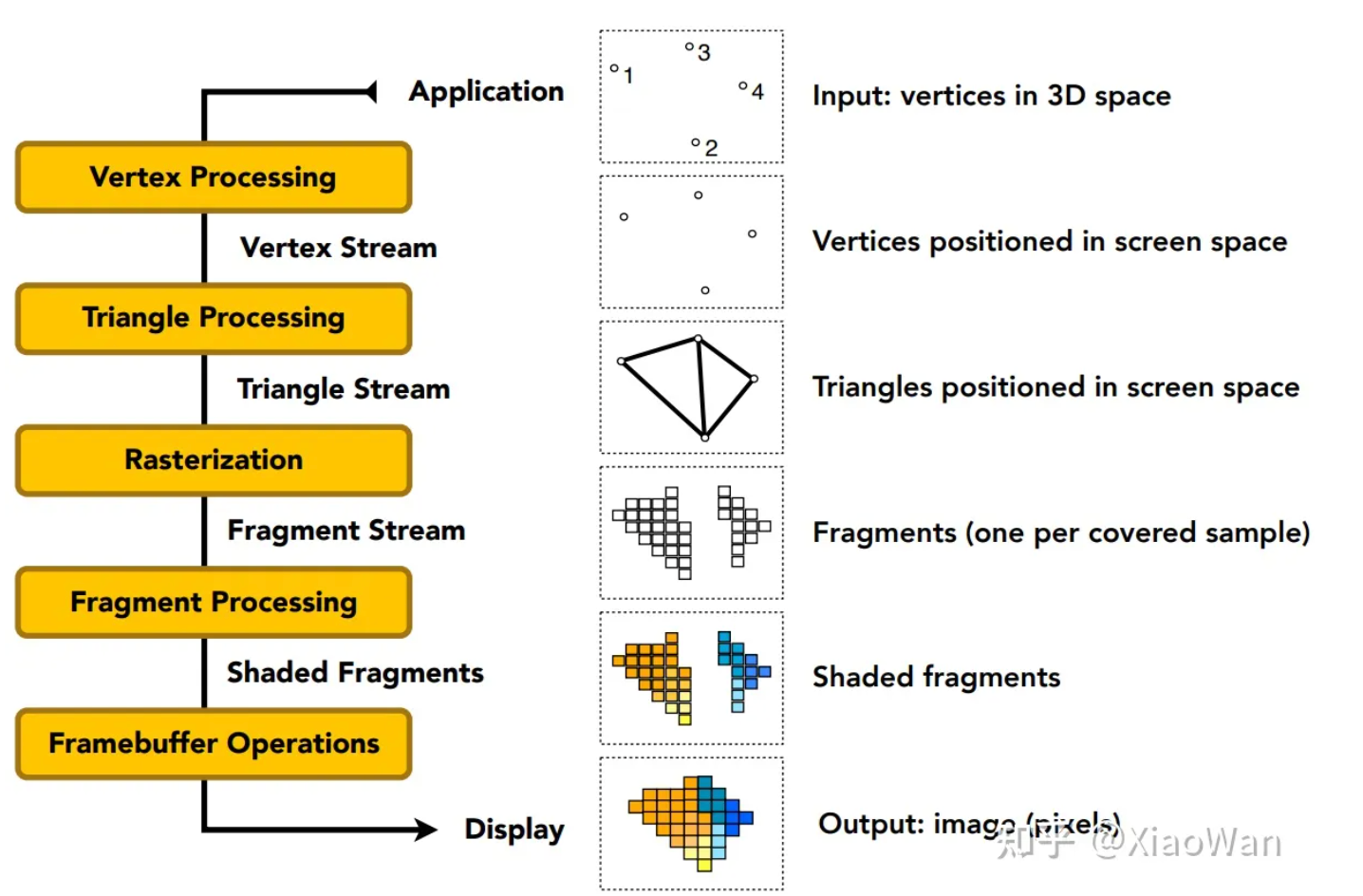
由于这些计算互相无关，则非常适合 GPU 的并发，所以看似计算量很大，确可以快速计算完成

Texture Mapping(纹理映射)

定义某个点的基本属性。三维上的点可以被映射到纹理坐标系中（UV 坐标、ST 坐标）

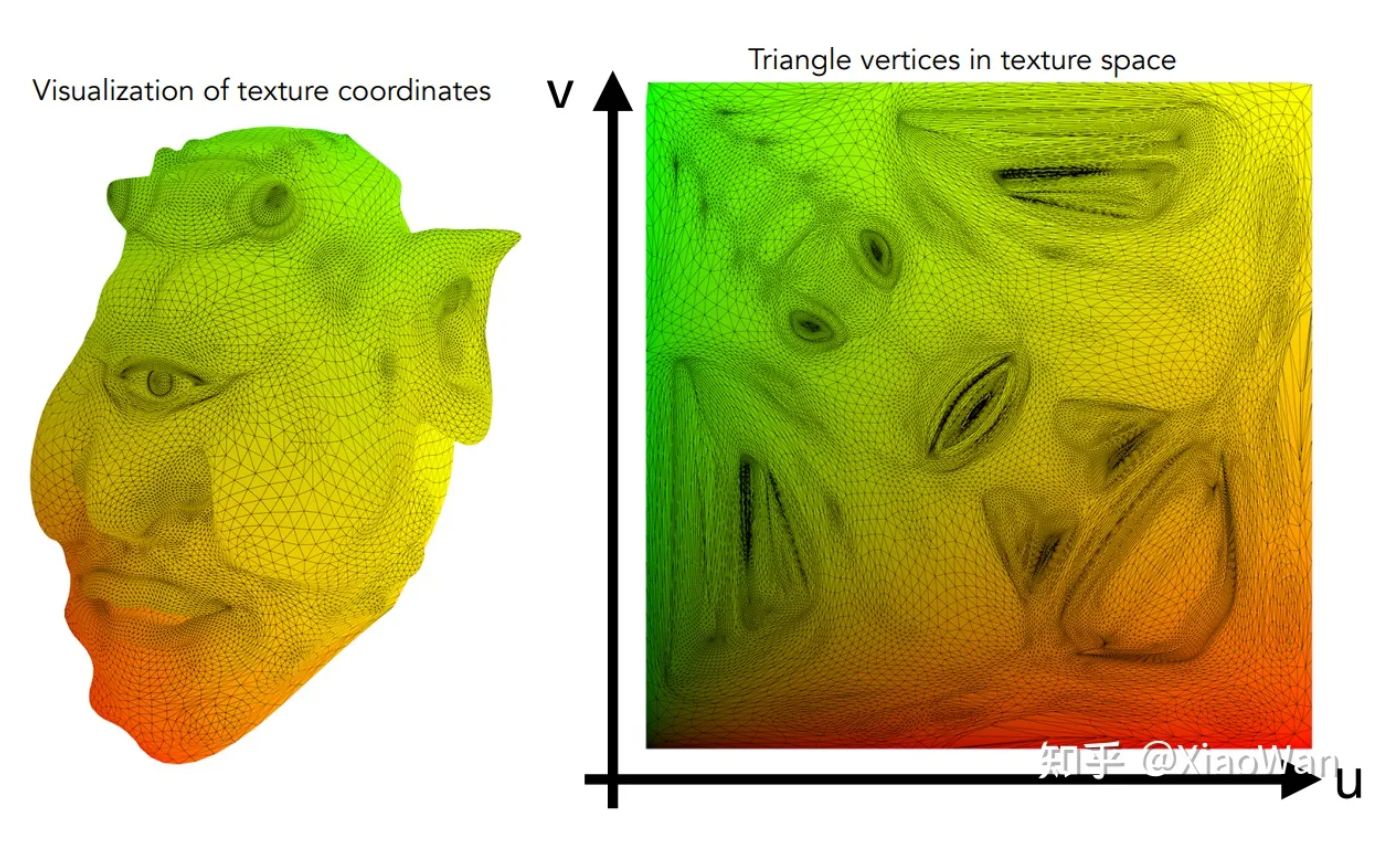
线性插值及应用

为什么会需要插值？为了获取平滑的过度效果 有哪些需要插值？纹理，坐标系，法向量

例如一个三角形，知道三角形的顶点，则三角形内任意一点都可通过三个点的插值计算而得

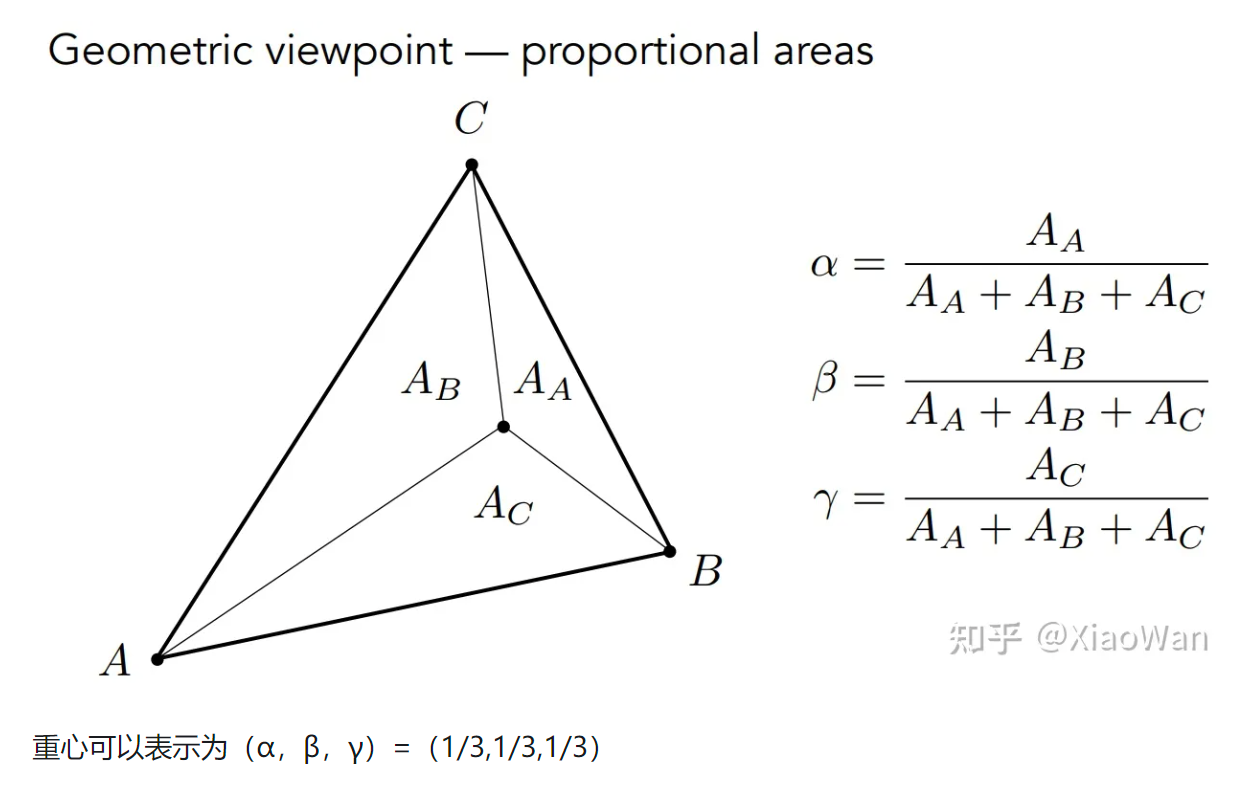
应用材质

将各个顶点，通过重心坐标映射到 UV 坐标内，UV 坐标对应的值，就是漫反射系数kdk_d

问题 1 纹理太小如何处理

当纹理太小了，不同的顶点映射的 UV 值不会是正好一个像素位置，例如可能映射为 (1.2,3,2)的像素位置。此时可以采用双线性插值或者三重线性插值，下图为双线性插值

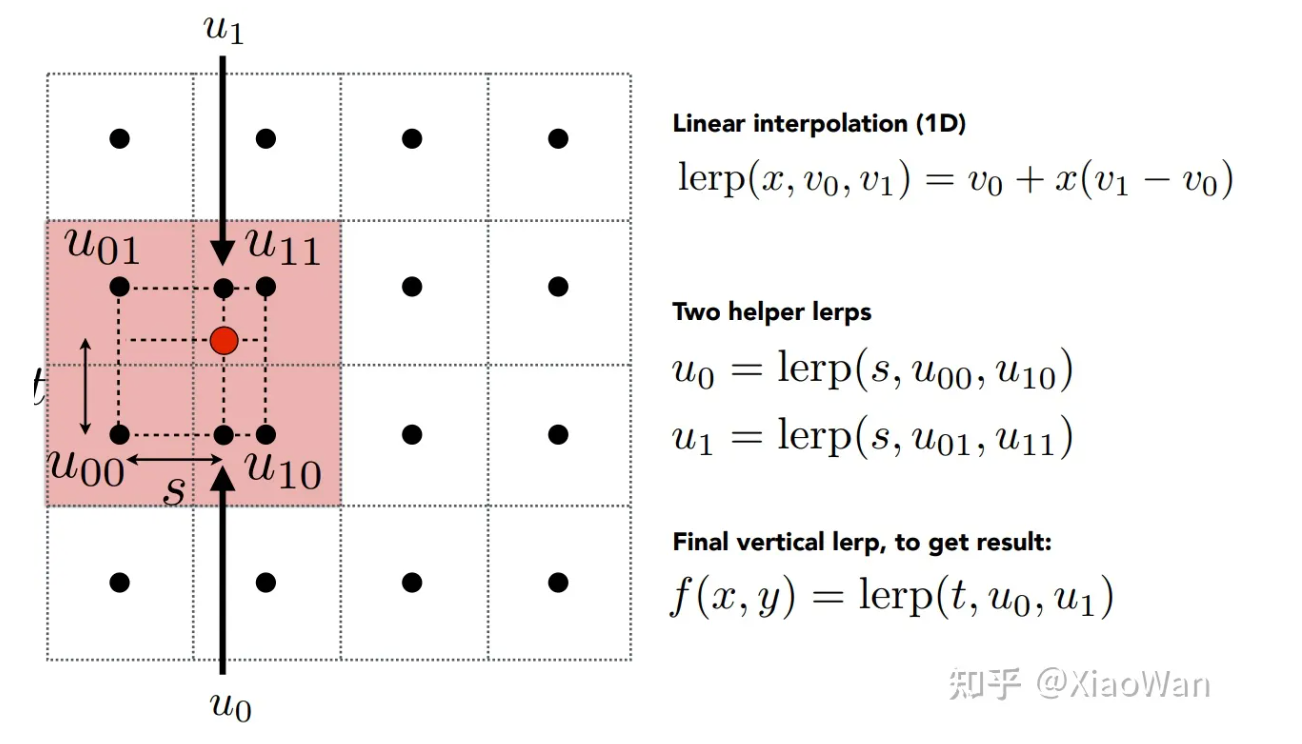
问题 2 纹理太大如何处理

纹理过大，会造成模糊，近处出现锯齿，远处出现摩尔纹。使用Mipmap来解决**，**在不同分辨率下，提供不同的纹理

  1. Level0 是原始的纹理图像，每提高一个 Level，则分辨率缩小一倍，利用相邻的四个像素进行平均
  2. Mipmap 会需要额外的 1/3 存储空间

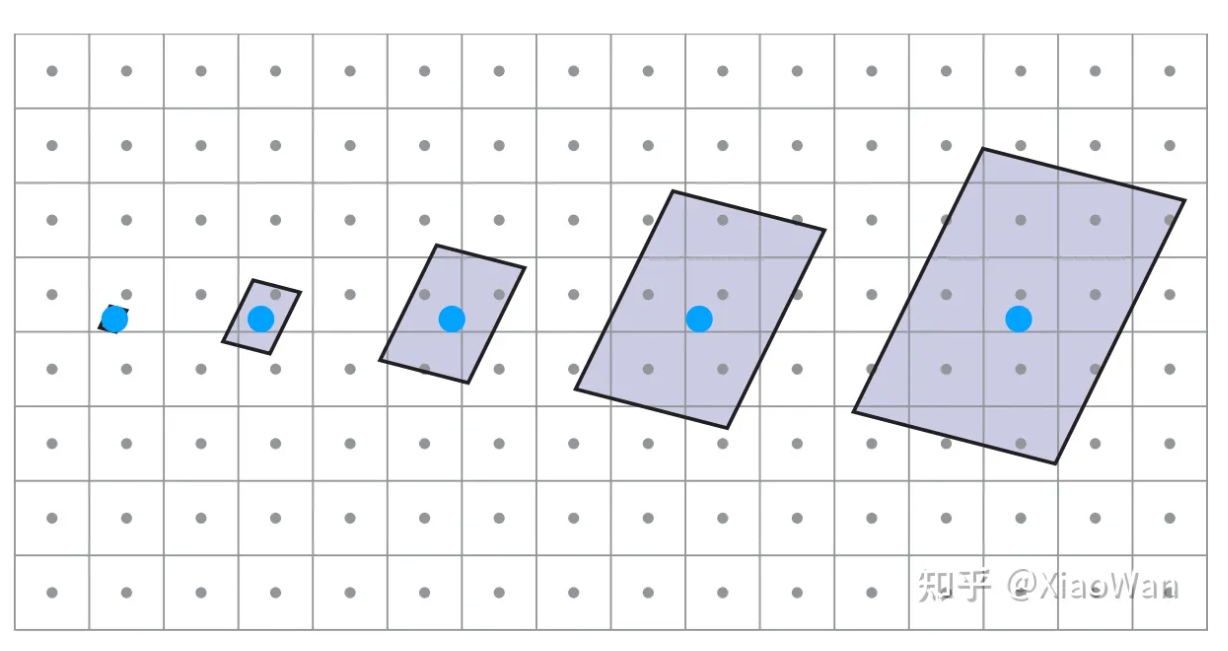
过渡不平滑

使用 Mipmap 会导致过度不平滑的问题，因为在 3D 中，由于计算而得不会恰好属于某一个层级，例如值可能为 1.2 曾。可采用 三线性插值，即在两层 Mipmap 先做双重线性插值，然后两层 Mipmap 再做线性插值

过度模糊

使用 Mipmap 可能会造成远处模糊，因为贴图基本为矩形，而 3D 中由于视角的问题，有可能是矩形，被拉伸，被压扁等等，导致如果在按照矩形去计算纹理的话，就会很模糊。使用多项异性过滤，即对 X,Y 采用不同比例的压缩

纹理映射的应用

纹理 = 内存 + 查询。纹理的数据会存储于内存中，我们可以对内存进行范围查询

球面环境映射

将环境光反射到球面

球面映射

将球面映射展开为平面，此时平面会出现扭曲

立方体映射

将环境光反射至正方图

凹凸贴图

以贴图来展示凹凸，而不用改变几何本身

三维纹理

Geometry(几何)

几何的表示方法

隐式

通过公式描述一个图形，例如f(x,y,z)=1f(x,y,z) = 1无需描述每一个点的位置。例如圆球的公式为x2+y2+z2=1x^2 + y^2 + z^2 = 1

优点

  1. 判断点是否属于图形较为容易

缺点

  1. 难以通过公式判断出图形的形状

显式

描述每一个点的位置。例如点云，多边形网格等待 优点

  1. 通过点可以判断出图形的形状

缺点

  1. 难以判断点是否属于图形，需要遍历所有的点

存储，表示一个几个图形，需要存储如下数据

  1. 点的位置
  2. 法线
  3. 纹理坐标

根据存储的如上数据，既可以绘制出一个图形

一些复杂的几何也是通过简单几个组合而成，组合计算一般为交集，并集，补集

贝塞尔曲线

给定一个起始点和**终止点**，中间给定若干个控制点来控制方向，由此绘制的光滑的曲线几位贝塞尔曲线

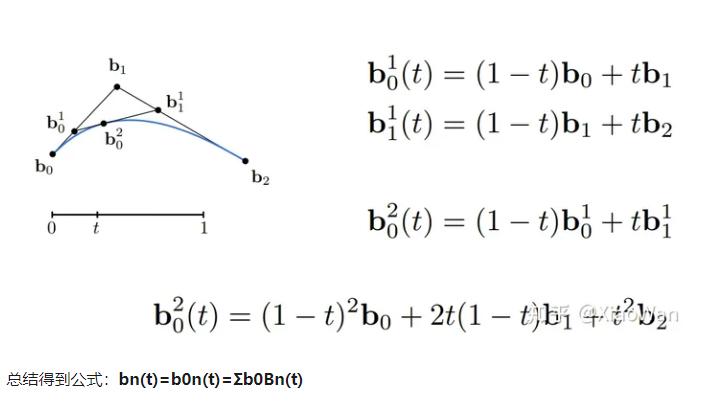
当控制点过度的时候，会影响绘制，一般采用分段贝塞尔曲线，例如可以以每四个控制点绘制曲线，再将其全部连接到一起

多边形网格

将面拆解为多边形（大多是三角形和四边形），存储顶点和多边形信息，

网格细分

网格面更多，模型更加精细

网格简化

  1. 让网格数更少，模型更加粗糙。
  2. 边坍缩，通过“二次误差度量”得到坍缩后最优的点

举个例子，当距离较远的时候，远处的模型看的不是很清楚， 没必要绘制的如此精细。

网格正规化

让网格中的三角形趋近于正三角形

Ray Tracing(光线追踪)

光纤追踪就是模拟光纤传播，在模拟的过程中计算每个像素的颜色（材质 + 颜色）

在计算光线追踪之前，需要做如下假设

  1. 假设光线是直线传播
  2. 假设光线之间不会互相干扰
  3. 假设光源是源源不断的发射光线

光线追踪的基本步骤

  1. 从观察点到成像平面的一个像素连接，发出一根光线到场景中
  2. 找到与场景中最先相交的点
  3. 该点与光源连接，判断该点的光照情况
  4. 根据判断结果，绘制该像素的颜色

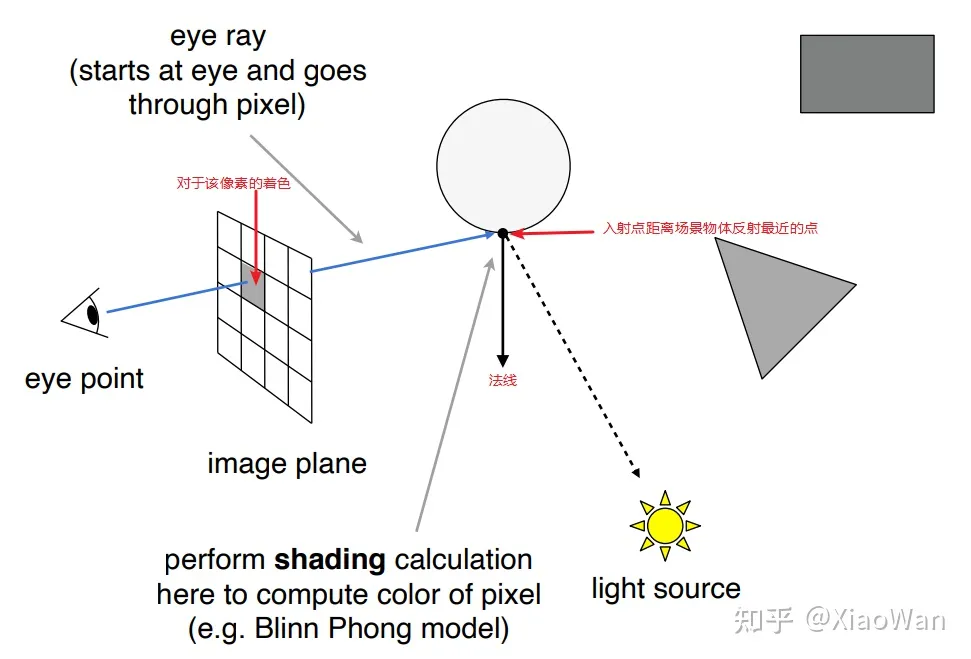
picture 0

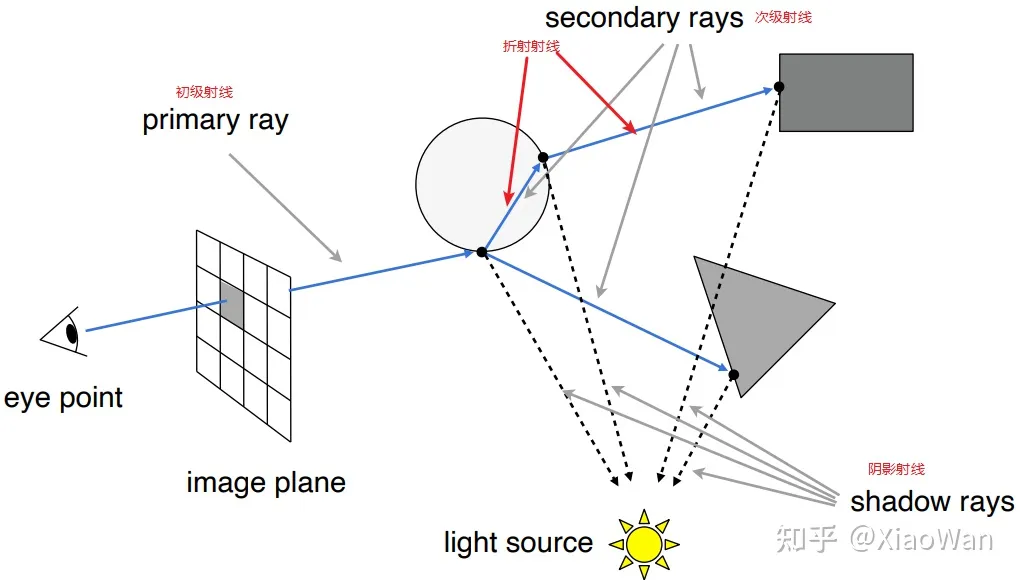
光线是会反射，折射的，所以需要对光线递归追踪，具备以下特点

  1. 光线的反射，折射
  2. 光线存在能量衰减
  3. 递归的最大次数限制，否则计算过程过于复杂

picture 1

阴影

在无光追之前，如何实现阴影呢

进行阴影的深度测试，一个物体或者一个区域被光源和视线观察到，有如下情况

  1. 光源可以照射到，视线可以看到
  2. 光源可以照射到，视线看不到
  3. 光源照射不到，视线可以看到
  4. 光源照射不到，视线也看不到

视线看不到的时，无需绘制，即只有在光源照射不到的时候，而视线可以看到的时候有阴影。但阴影的深度测试有如下缺点

  1. 硬阴影视线较为简单，但是软阴影需要在阴影深度测试结构后，再使用阴影软化技术
  2. 由于 Shadow map 分辨率的问题，容易出现锯齿，也可用阴影软化技术优化
  3. 由于浮点数精度问题，在判定光源和视线时容易出现问题

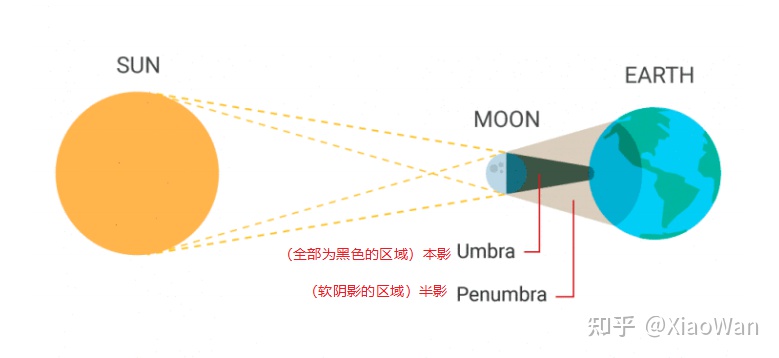
可以更加好的实现如下效果，效果虽好，但是相较于光栅化性能较低

  1. 软阴影
  2. 毛玻璃的反射效果
  3. 间接光照（经过反射的光）

光纤传播的假设

  1. 光纤沿直线传播（虽然是错误的）
  2. 光线之间不会发生碰撞（虽然是错误的）
  3. 光线是从光源不断的传播到可视区域

Whitted-Style

光线的投射

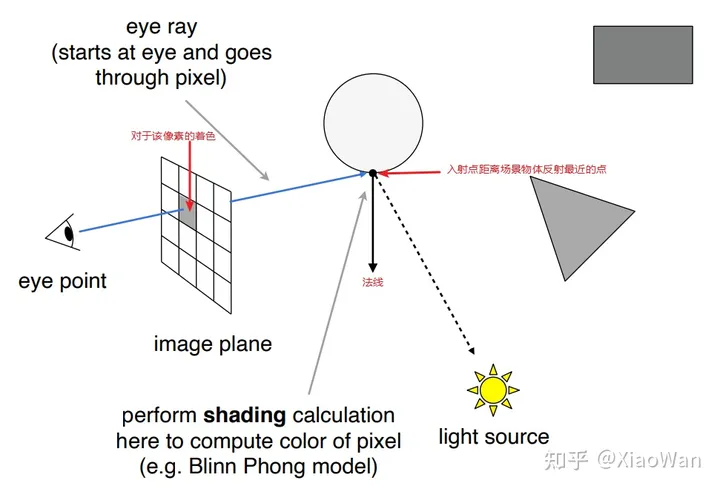
  1. 从视点到像素连接，发出一根光线到场景中
  2. 找到与场景中最先相交的点
  3. 该点与光源连接，判断该点的光照情况
  4. 计算着色器

递归光线追踪

光线不仅会反射，还会折射，所以需要对光线递归追踪，具备以下特点

  1. 反射，折射存在能量衰减
  2. 反射，折射次数需要限制，不然计算量过大

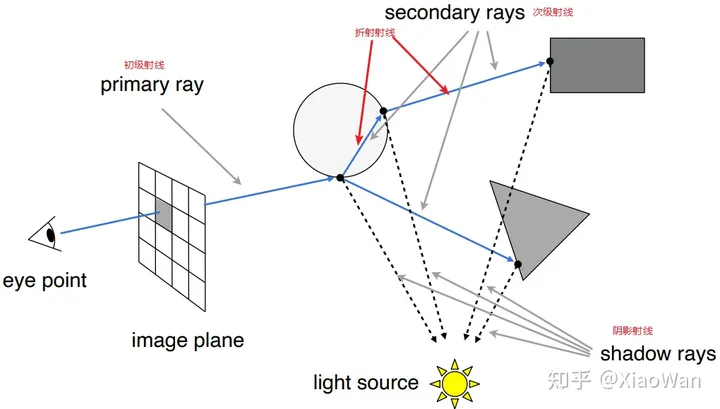
确定光线与场景的交点

  1. 隐式几何：将光线带入方程式计算
  2. 显示几何：遍历场景中的所有点，计算光线与点之间的距离，找到最近的一个点。但是这种方法太慢了，使用*轴对齐包围盒(AABB)*来加速计算

轴对齐包围盒(AABB)：只有 入包围盒 && 出包围盒 同时满足，才表示光线与场景有交点

当物体在场景分布不规律时，如何划分包围盒

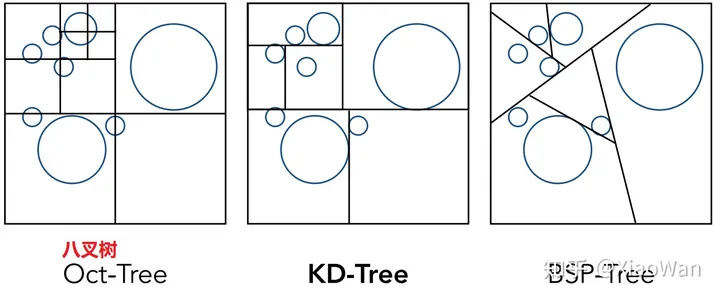
  1. 八叉树
  2. KD 树
  3. BSP 树

辐射度量学

Whitted-Style 不够真实，引入辐射度量学